OpenStax College Physics for AP® Courses, Chapter 5, Problem 5 (Problems & Exercises)

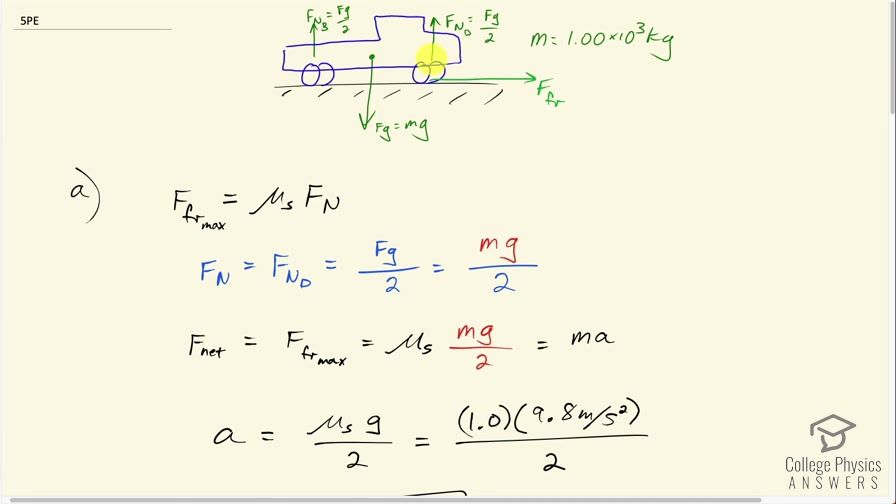
This is College Physics Answers with Shaun Dychko. This is a utility truck which is two-wheel drive and we are told that half of the weight of the truck is supported by the drive wheels and so there is a force of gravity downwards equal to mass times gravitational field strength and that gravity downwards is compensated for by the total normal force upwards and the total normal force upwards has to equal the gravity downwards because the truck is not accelerating vertically. So we are told that half the weight is supported on the drive wheels and that's why this normal force has a subscript D on it for 'drive wheels' and we are dividing by 2 because half the weight is supported by these wheels. This 2 is not the number of wheels... even though there are two of the wheels, it's just coincidence that the number of wheels is 2 and this denominator is 2— this denominator 2 comes from the fact that half of the weight is supported by the drive wheels. Had there been three wheels in the front that were drive wheels... of course you will never see that but you know supposing, it was true there were three drive wheels... well, nevertheless this reaction would still be force of gravity divided by 2 because half the weight is supported by the drive wheels however many drive wheels there are... doesn't matter... it's how much weight is supported by those wheels that is important. Okay! There's also a normal force in the back wheels equal to the remainder of, you know, gravity that needs to be supported by the normal force and that's going to be F g over 2 but that's not important there, what's important is the total normal force on the drive wheels. Okay! The question in part (a) is what is the maximum acceleration of the truck? And so there's this friction force that's going to propel it forward and the friction force at its maximum will be the coefficient of static friction between the tires and the road multiplied by the normal force and this is F N D here for 'drive wheels'. And the normal force on these drive wheels is the weight of the truck—F g—divided by 2 and that is mg over 2 where the force of gravity is mass of the truck multiplied by gravitational field strength. Okay! So the net force horizontally is the friction force which is going to be at its maximum for this calculation and so that is the coefficient of static friction times mg over 2 and that's going to be mass times acceleration because that's Newton's second law and the mass will cancel out on both sides, we will divide both sides by m and we are left with acceleration after we switch the sides around acceleration on the left equals μ sg over 2 on the right so we did a switcheroo here to get to this line here— and the coefficient of static friction will be 1.0 because that's the coefficient of static friction for rubber on dry concrete— 1.0 times 9.8 meters per second squared— acceleration due to gravity— divided by 2 and that's 4.9 meters per second squared will be the acceleration of the truck when it is two-wheel drive. Okay! Part (b) asks us will the metal cabinet in the wooden flatbed of the truck slide in this scenario when the truck is accelerating at 4.90 meters per second squared? So here's a free-body diagram of the cabinet and it's a simple diagram that ignores the wheels of the truck and so on... this question is just to do with the cabinet and the surface of the flatbed... that's all that matters here. So this F N is the normal force on the cabinet, F g here is mass of the cabinet times acceleration due to gravity— notice that I sometimes call this factor acceleration due to gravity and other times I call it gravitational field strength both terms are correct... kind of depends what the context of your question is. Okay—we are going to call it acceleration due to gravity most of the time even though I think I said gravitational field strength up above. Okay! So the letters here are different than for part (a) so m here is mass of the cabinet whereas m up here was the mass of the truck but the mass of the cabinet, it's going to cancel out anyway. Alright! So the normal force upwards equals force of gravity downwards and so it is the mass of the cabinet times g because there is no vertical acceleration. And the maximum friction force is the coefficient of static friction— in this case, it's going to be the coefficient between metal and wood so this is a different coefficient of static friction than we had in part (a) so I could have put another subscript on here to say coefficient of static friction for the truck tires or something like that but just to be a bit more speedy I am just reusing the regular μ s with no other subscript, I am just saying with words what I mean here and this is the coefficient of static friction between metal and wood. So we multiply that by the normal force which is mg substituting that in here and we have the maximum friction force is also the net force horizontally and so that's going to equal the mass of the cabinet times its maximum acceleration. So we have mass of the cabinet times its maximum acceleration equals μ smg because both of these are equal to the maximum friction force and we can divide both sides by m and we get maximum acceleration of the cabinet then is the coefficient of static friction times acceleration due to gravity— and this is 0.5 for the coefficient of friction... that is metal on wood— and we multiply that by 9.80 meters per second squared and that is 4.9 meters per second squared. So because the acceleration of the truck is not more than the maximum possible acceleration for the cabinet that means the cabinet will not slip although we are right on the threshold; this is the very maximum that the cabinet can sustain for acceleration and the truck is indeed going at exactly that acceleration so this is the threshold between when it will and it will not slip but since it begins not slipping, it will continue to not slip and there we go! Part (c) says answer both these questions assuming four-wheel drive. So now the normal force on the drive wheels will equal the total weight of the truck mg and again it doesn't matter how many wheels are involved, what matters is that the drive wheels... be it 4, 6 or whatever... I mean it is common to have 6 drive wheels or you know, you can have a truck with a dually wheels in the back where there's a pair of wheels so you can have six tires driving it maybe. In any case, it doesn't matter... what matters is what is the total weight supported by the wheels that will be driving and the answer is the total weight of the truck mg. Okay! So the maximum friction force then is coefficient of static friction times the normal force on the drive wheels, which is equal to the weight mg and this maximum friction force is the net force and so it is mass of the truck times its maximum acceleration so both of these are each equal to the maximum friction force and so we can equate these two things here. Okay! And then divide both sides by the mass of the truck and we are left with maximum acceleration is coefficient of static friction between the tires and the concrete times acceleration due to gravity— and we already looked up that coefficient of static friction for rubber on dry concrete is 1.0— times 9.8 meters per second squared, which is 9.8 meters per second squared. So the four-wheel drive will cause the truck to have double the maximum acceleration so yay for four-wheel drive! Will the cabinet slip? Yes because now the truck is going to accelerate at 9.8 meters per second squared which exceeds the maximum possible acceleration for the cabinet because even though the truck is two-wheel drive vs. four-wheel drive, nothing's changed for the picture for the cabinet. As far as the cabinet's concerned, there's just a cabinet and there's a wooden flatbed and what is the maximum acceleration that the static friction force can sustain between these two objects? And we already calculated that, it was 4.9 and that's not going to change and so yes the cabinet will slip because the truck is going to accelerate faster than the cabinet possibly can. And there we go!