Question
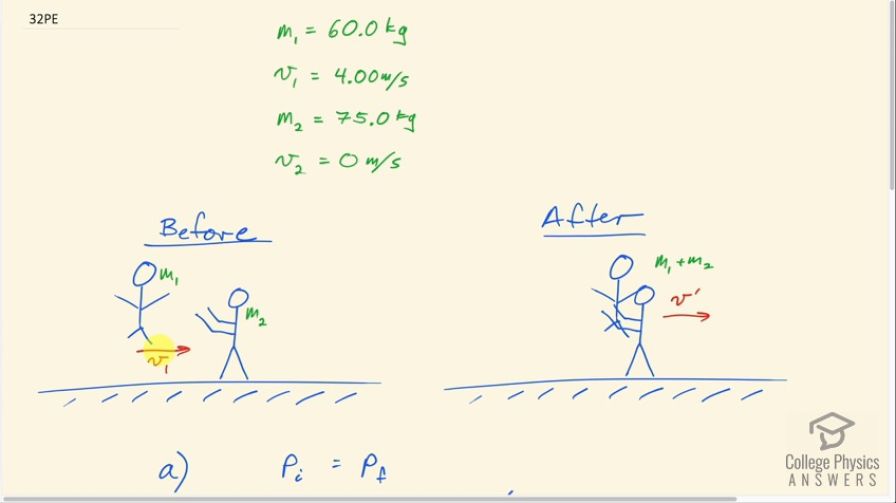
During an ice show, a 60.0-kg skater leaps into the air and is caught by an initially stationary 75.0-kg skater. (a) What is their final velocity assuming negligible friction and that the 60.0-kg skater’s original horizontal velocity is 4.00 m/s? (b) How much kinetic energy is lost?
Final Answer
- of kinetic energy was lost.
Solution video
OpenStax College Physics, Chapter 8, Problem 32 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
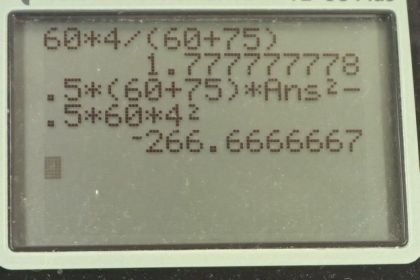
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A figure skater with mass m 1— 60 kilograms— leaps into the air going at an initial speed of 4 meters per second horizontally towards this other skater that's going to catch her and he has a mass of m 2— which is 75 kilograms— and he's initially at rest. So the total momentum is shown in this picture and it's only this particular skater that has any momentum— this leaping one— and so that initial momentum then is going to be m 1v 1. The total momentum after catching is going to be the mass of this complete system which is the total mass of the two skaters, m 1 plus m 2, and they are going to be moving together with some speed that we'll call v prime. I suppose I should be using the word 'velocity' and not 'speed' but in any case since this is all in one dimension and all in the same direction, the distinction doesn't matter that much but let's use the correct word so 'velocity.' Alright! We are wanting to find what is the velocity after catching so v prime is the question. So we have m 1v 1—initial total momentum—equals m 1 plus m 2—the total mass— multiplied by v prime is the total momentum final and we'll solve for v prime by dividing both sides by m 1 plus m 2 and then switch the sides around. So we have v prime then is m 1v 1 over m 1 plus m 2 so that's 60 kilograms times 4 meters per second divided by 60 plus 75 which is 1.78 meters per second. And then part (b) asks us how much kinetic energy is lost in this interaction... lost by this skater being caught and so the total final kinetic energy is one-half times the mass of the two skaters together multiplied by their common velocity v prime squared and then we'll take from that the initial velocity that the individual skater had by herself when she was leaping that is one-half m 1v 1 squared. So that's one-half times the total mass times this speed that we calculated in part (a), and velocity again of course, squared minus one-half times 60 kilograms times 4.00 meters per second squared which is negative 267 joules. This negative indicates that kinetic energy has been lost; the final kinetic energy is less than the initial. So 267 joules of kinetic energy was lost.