Question
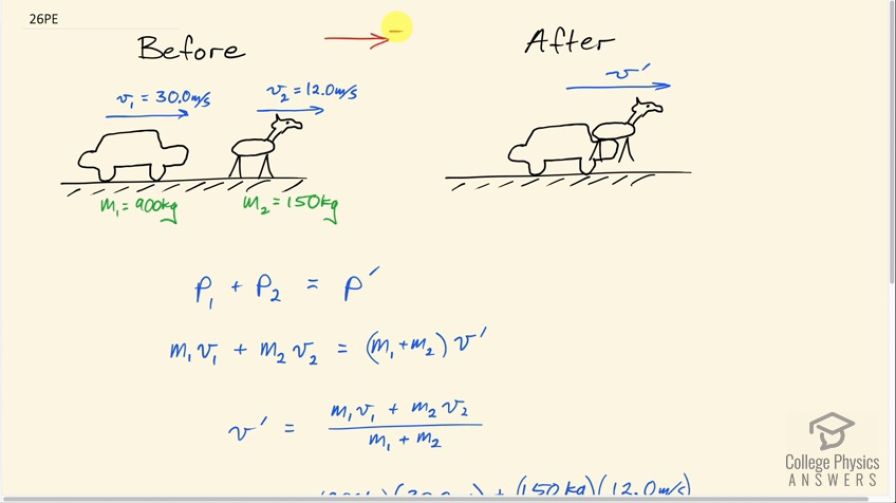
What is the velocity of a 900-kg car initially moving at 30.0 m/s, just after it hits a 150-kg deer initially running at 12.0 m/s in the same direction? Assume the deer remains on the car.
Final Answer
Solution video
OpenStax College Physics, Chapter 8, Problem 26 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A car is moving to the right with a velocity of positive 30.0 meters per second—we are taking the 'right' to be the positive direction— and it's going to collide with a deer that's running in the same direction with a speed of 12.0 meters per second and the car has a mass of 900 kilograms and the deer has a mass of 150 kilograms. After the collision, we assume that the deer sticks to the car so afterwards, there's only one object— it's this deer-car thing— and that is going to be moving with some velocity v prime So we are going to write down our conservation of momentum expression here and so the total momentum initially, P 1 plus P 2, that is the momenta before collision, equals the total momentum afterwards and there's only one object so there's only one term here, we'll call it P prime. So P 1 is the momentum of the car so that's mass 1 times velocity 1 and then plus the momentum of the deer which is mass 2 times velocity 2 and that's going to equal the total mass of this system here which is m 1 plus m 2 multiplied by its speed v prime. Our job is to solve for the speed of the car, which is v prime, and so we'll divide both sides here by m 1 plus m 2 and then switch the sides around as well and we get v prime then is m 1v 1 plus m 2v 2 over m 1 plus m 2. So that's 900 kilograms times 30.0 meters per second plus 150 kilograms times 12.0 meters per second divided by the total mass giving us a speed of 27.4 meters per second and that's a velocity actually—it's positive and it's to the right—and there we go!
Comments
if the deer is running in the same direction wouldn’t you multiply buy -12 in the equation


