Question
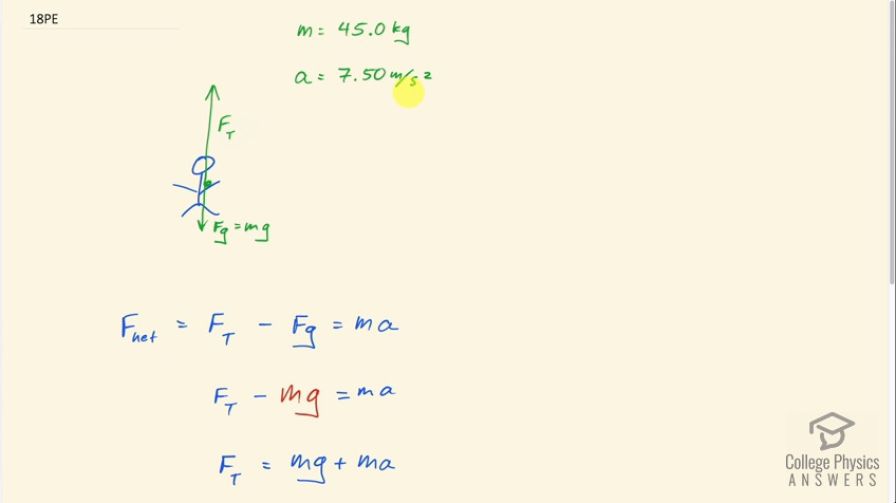
What force does a trampoline have to apply to a 45.0-kg gymnast to accelerate her straight up at ? Note that the answer is independent of the velocity of the gymnast—she can be moving either up or down, or be stationary.
Final Answer
Solution video
OpenStax College Physics, Chapter 4, Problem 18 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. What force does a trampoline need to apply on a gymnast to accelerate the gymnast upwards at a rate of 7.5 meters per second squared, given that the gymnast's mass is 45 kilograms. Here's a free body diagram showing the gymnast with the force upwards labeled f subscript T for trampoline, and there's a force downwards on them the force due to gravity, which is their mass times gravitational field strength or acceleration due to gravity depending on how you like to name this letter g. The net force vertically is going to beF T upward so it's positive, and then minus the force of gravity downwards and all of that equals mass times acceleration. We can replace Fg with mg, and then we're going to solve for F T by adding mg both sides. We have the forest supplied by the trampoline upwards is m factored out here because it's the common factor times g plus a that's 45 kilograms times 9.8 meters per second squared plus 7.5 meters per second squared, which is a force of 779 newtons.
Comments
Hello, What in the question implies that the other acting for on her is gravity? or if she is in contact with the trampoline, why is normal force not applied to her?
Hi johnrbolo, it's safe to assume gravity is always part of a question, and the acceleration due to gravity is unless the question gives some kind of context that might suggest otherwise, such as "in deep space" or "on the moon". The normal force is the force applied by a surface perpendicular to the surface - that would be another way of labeling the force due to the trampoline. They are the same.
All the best,
Shaun


