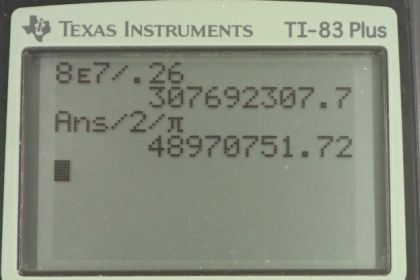
An automobile with 0.260 m radius tires travels 80,000 km before wearing them out. How many revolutions do the tires make, neglecting any backing up and any change in radius due to wear?
Solution video
OpenStax College Physics, Chapter 6, Problem 3 (Problems & Exercises)

Calculator Screenshots
Comments
80000000/.260 is not equal to 307690000. It is equal to 307692307.7
Hi tahir.va3, thank you for the comment. You're quite right, but since there is only going to be one significant figure in the final answer, there's no need to carry too many significant figures in the intermediate calculations. While I often mention "don't round until the final answer" in order to avoid intermediate rounding error, it seems safe enough to carry 4 additional significant figures in the intermediate calculation since surely it won't make a different to the final answer with only one sig. fig.
All the best,
Shaun
It's also much simpler to simply find the circumference of the tire and then divide the distance by that. I understand it's for the sake of teaching physics but it seems silly to give a question like this. Without this video I would have not known to use the arc length.
Hello, I keep getting 5*10^8 and not 5*10^7.