Question
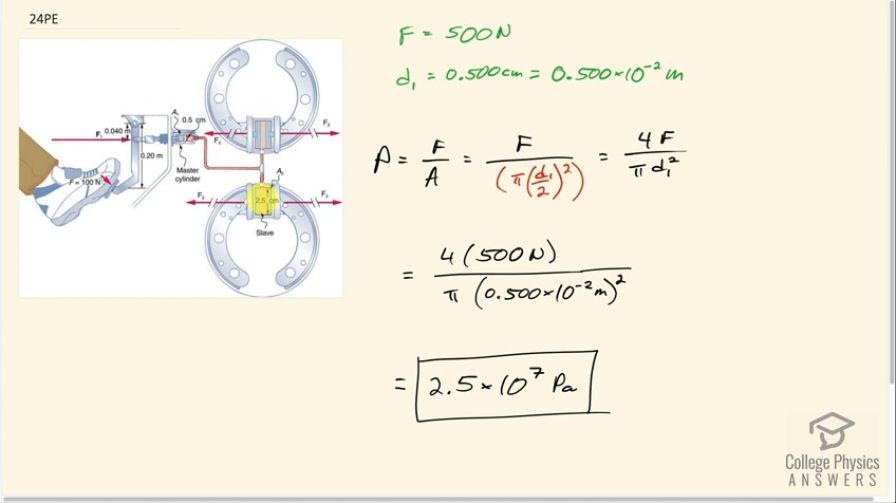
How much pressure is transmitted in the hydraulic system considered in Example 11.6? Express your answer in pascals and in atmospheres. Example 11.6 Consider the automobile hydraulic system shown in Figure 11.13. A force of 100 N is applied to the brake pedal, which acts on the cylinder—called the master—through a lever. A force of 500 N is exerted on the master cylinder. Pressure created in the master cylinder is transmitted to four so-called slave cylinders. The master cylinder has a diameter of 0.500 cm, and each slave cylinder has a diameter of 2.50 cm.
<b>Figure 11.13</b> Hydraulic brakes use Pascal’s principle.
Figure 11.13 Hydraulic brakes use Pascal’s principle.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

2.5×107 Pa2.5\times 10^{7}\textrm{ Pa}
2.5×107 Pa×1 atm1.013×105 N/m2=147 atm2.5\times 10^{7}\textrm{ Pa} \times \dfrac{1 \textrm{ atm}}{1.013\times 10^{5}\textrm{ N/m}^2} = 147\textrm{ atm}
Note: I forgot to express the answer in atmospheres in the video, but it's shown here in the final answer.

Solution video

OpenStax College Physics, Chapter 11, Problem 24 (Problems & Exercises)

OpenStax College Physics, Chapter 11, Problem 24 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 11, Problem 24 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We need to find the pressure in this hydraulic break system. So we can find the pressure anywhere... you know, in the slave cylinders or in the master cylinder because the pressure is the same throughout— that's what Pascal's principle says— and so we'll consider the pressure created by the master cylinder because we have information about it. We know that 500 newtons ends up being applied to this master cylinder and the diameter is 0.500 centimeters which we convert to meters by noticing that the prefix 'centa' means times 10 to the minus 2. So pressure is force divided by that area and it's a circular cross-section here— this cylinder is circular— and so the area is π times its radius squared and its radius is half its diameter so I have written d over 2 here and squared and then this works out to 4 times the force divided by π times the diameter squared. That's 4 times 500 newtons divided by π times 0.500 times 10 to the minus 2 meters squared which is 2.5 times 10 to the 7 pascals.

Comments

Hi Juliana, thank you for the comment. The answer is not wrong... strictly speaking I didn't divide the diameter by 2, but rather I multiplied the expression by 4 instead. Please considering reviewing the part at 0:46 in the video where I mention this. Granted, the algebra might have been too fast: dividing a factor in the denominator by 2 squared is the same as multiplying the numerator of the main fraction by 4. Consider thinking of this as multiplying the top and bottom of the main fraction by 4. The 4 cancels in the denominator of the main fraction.
Hope this helps,
Shaun