Question
People who do very detailed work close up, such as jewellers, often can see objects clearly at much closer distance than the normal 25 cm.
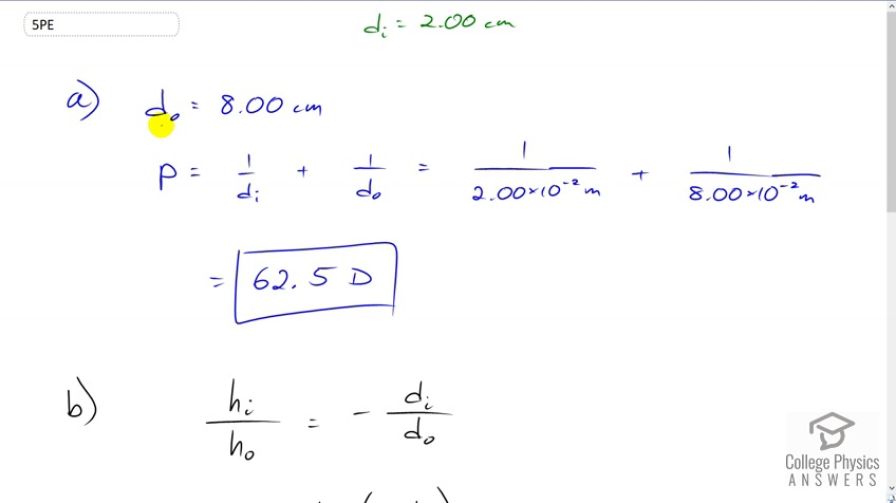
(a) What is the power of the eyes of a woman who can see an object clearly at a distance of only 8.00 cm?
(b) What is the size of an image of a 1.00 mm object, such as lettering inside a ring, held at this distance?
(c) What would the size of the image be if the object were held at the normal 25.0 cm distance?
Final Answer
- 62.5D
- -0.250 mm
- -0.0800 mm
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 5 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The power of the eye is the reciprocal of the image distance plus the reciprocal of the object distance. So, we're told that the jeweler holds some jewelry eight centimeters in front of their eye, that's their near point, I suppose. And, it's much closer than the average person's eyes because they have a lot of practice and maybe either accommodation of their eye is more powerful than the average eye since they are using the muscle to change the lens shape more than the average person. So, power is then reciprocal of image distance which we're told is always two centimeters. That's the distance between the lens and the retina. So, we take the reciprocal of that in units of meters and add that to one over eight times ten to the minus two meters for the object distance and that gives a power of 62.5 diopters. Part B asks us what is the image height for a one millimeter detail on the ring. So, we know that magnification is image height divided by object height and magnification also is the negative of image distance over object distance. So, we can solve for Hi by multiplying both sides by Ho. So, image height is object height times negative of image distance divided by object distance. So, that's one millimeter times negative two centimeters divided by eight centimeters and that gives negative 0.250 millimeters. Now, the units here are a bit interesting. Often, and usually in formulas, we change the units into meters, kilograms, and seconds, MKS units. But in this case, the centimeters, you can see are going to cancel, and you're going to be left with millimeters. So, we can just jump straight to millimeters in our answer without needing to convert to meters. Now in part C, if the object distance was instead 25 centimeters and not 8 centimeters, what would the height of the image be? So, we have the same detail we're looking at is this one millimeter detail on the ring. And, we multiply that negative two centimeters divided by 25 centimeters, which is negative 0.0800 millimeters. And so, held at 25 centimeters, the image on the retina is much smaller and so, there will not be as much observable detail, which is why we bring things closer to look at them in more detail because bringing things closer increases the size of the image on the retina.
