Question
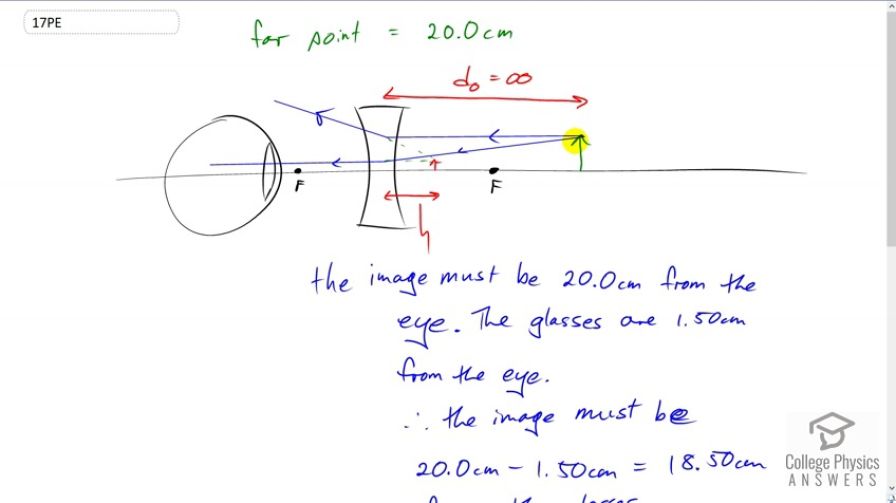
A very myopic man has a far point of 20.0 cm. What power eyeglasses, positioned 1.50 cm from his eyes, will correct his distant vision?
Final Answer
-5.41 D
Solution video
OpenStax College Physics for AP® Courses, Chapter 26, Problem 17 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
his is College Physics Answers with Shaun Dychko. This person has myopia, which means they have a far point that is less than infinity. Their far point is 20 centimeters and that means they can't see anything that's further away than 20 centimeters. Now, the purpose of these glasses is to position the object and replace it with an image that is located at the far point of the eye. So, the eye can't see this object on its own, and so instead, the eye is going to be observing an image of the object and the image is going to be positioned by this lens at this distance away from the eye so that the eye can see it. And, this distance that I have highlighted in blue here is the far point distance of 20 centimeters. So, this is the purpose of glasses, is to reposition the object as an image some place where the eye can see it. So, given that the image has to be 20 centimeters form the eye, and we're told that the glasses are one and a half centimeters from the eye, so this distance here is one and a half centimeters, then that means the image distance, which is the distance between the lens and the image, has to be 20 centimeters minus this one and a half centimeter gap between the eye and the lens for an image distance of 18.5 centimeters from the lens to the image. Now, because this image is on the same side of the lens as the object, it's on the right hand side here just the same as the object is, this is a virtual image. For that reason, we'll put a negative sign in front of this image distance. So, the image distance is negative 18.5 centimeters. So, the power of the lens that's required to solve this person's vision problem is going to be one over this image distance plus one over the object distance. Now, the object is going to be at infinity, because we're looking at an object that is really far away, so this term becomes zero. And so, the power is going to be the reciprocal of the image distance. So, that's one over negative 18.5 times ten to the minus two meters, which is a power of negative 5.41 diopters.
