Question
(a) A person's blood pressure is measured to be 120±2 mm Hg120 \pm 2 \textrm{ mm Hg} . What is its percent uncertainty? (b) Assuming the same percent uncertainty, what is the uncertainty in a blood pressure measurement of 80 mm Hg?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 2%2\%
  2. 1 mm Hg1 \textrm{ mm Hg}

Solution video

OpenStax College Physics, Chapter 1, Problem 20 (Problems & Exercises)

OpenStax College Physics, Chapter 1, Problem 20 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

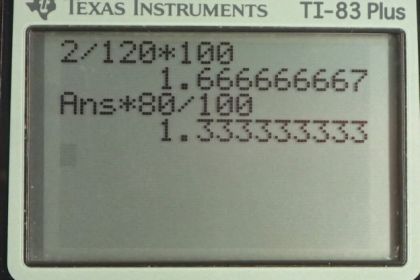
Calculator Screenshots

  • OpenStax College Physics, Chapter 1, Problem 20 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. A blood pressure measurement is 120 millimeters of mercury plus or minus 2 millimeters of mercury and the question in part (a) is what is that percent uncertainty? So equation number 8 in chapter 1 tells us percent uncertainty is the uncertainty in the measurement or absolute uncertainty which in this case is 2 divided by the measurement itself which in this case is 120 times a 100 percent and then we can rewrite this with the letters that are relevant to this particular problem with letter P instead of letter A and we substitute in numbers. So that's 2 milliliters of mercury error divided by 120 milliliters mercury which is the measurement times a 100 percent giving 1.67 percent but that's not our final answer because our error has only one significant figure and so our percent uncertainty also should have only one significant figure so we write 2 percent is our final answer. In part (b), we are asked, you know, given a measurement of 80 milliliters of mercury and the same percent error, what would the absolute error be? So percent uncertainty is the error in the pressure divided by the pressure times 100 percent and we have to rearrange this to solve for δP. So we'll multiply both sides by the pressure and divide both sides by 100 percent and then switch the sides around as well. So the error then in the measurement is gonna be the percent uncertainty times the pressure divided by 100 percent. Now I'm not writing 2 percent as the percent uncertainty here because we always want to use unrounded numbers in subsequent calculations; we don't want to use 2 percent here because that would be intermediate rounding error, you always want to use unrounded numbers so 1.67 is the number to use here and then we'll do our rounding at the very end. So 1.67 percent times 80 millimeters of mercury divided by 100 percent is 1.336 millimeters of mercury and this number should have only one significant figure because this measurement has only one significant figure. So one millimeter mercury is the error for an 80 millimeter mercury given the same percent error as we had up here for the 120 millimeters of mercury measurement.

Comments

Why does the absolute uncertainty affect the sig figs. No matter what you will not get more sig figs since it's a whole number.

Hi Ren, I'll try to answer this, but I might need a better understanding of what you're asking. The absolute uncertainty of 2 mm has one significant figure, but the fact that it's a whole number isn't relevant. If the uncertainty had hypothetically been 0.2 mm, that would have one significant figure also. Sometimes errors are estimated with greater precision, as in another hypothetical example 2.0 mm, which has two significant figures. Had the absolute uncertainty been estimated as 2.0 mm, then the percent error calculated in part (a) would have been written as 1.7% instead of 2%, and part (b) would have been 1.3 mm instead of 1 mm.

If that doesn't answer your question, just let me know.
All the best,
Shaun