OpenStax College Physics, Chapter 23, Problem 106 (Problems & Exercises)

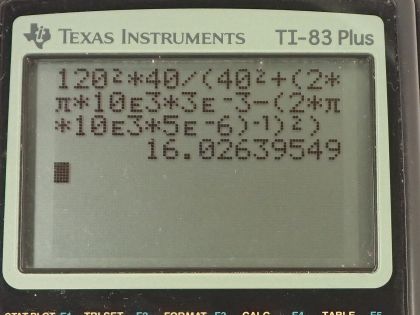
This is College Physics Answers with Shaun Dychko. Looking to example [23.14], we can collect some information about the circuit involved and then we are gonna figure out its average power at 10.0 kilohertz. So the resistance is 40.0 ohms; the inductance is 3.00 millihenries, which is 3.00 times 10 to the minus 3 henries; the capacitance is 5.00 microfarads, which is 5.00 times 10 to the minus 6 farads and the RMS voltage is 120 volts. So we are gonna use this formula to answer the question but there are a lot of steps involved in substituting for each of the factors here. The RMS current is the RMS voltage divided by the impedance and the cosine Φ is power factor and it is the resistance divided by the impedance and we can make a substitution for each of these factors as shown here in red. So I have substituted for the RMS current and I have substituted for the power factor. This works out to V rms squared times resistance divided by impedance squared. Now impedance is the square root of the resistance squared plus the inductive reactance minus the capacitive reactance squared but since we have Z squared here, we can square both sides of this and Z squared then is R squared plus X L minus X C squared and so this is what we can substitute in place of Z squared and we do that here. So now let's figure out expressions for these reactances then. The inductive reactance is 2π times frequency times inductance and the capacitive reactance is 1 over 2π times frequency times capacitance which I just felt like writing as 2πfC to the power of negative 1, which makes the reciprocal of this as the same as this. So substituting for X L and X C, we have this line here now so we have V rms squared times resistance divided by resistance squared plus 2πf times inductance—this is a substitution for the inductive reactance— and then we have 2πfC to the negative 1— that's a substitution for the capacitive reactance and then we can plug in numbers and get our answer. So we have 120 volts—RMS voltage— times 40.0 ohms divided by 40.0 ohms squared plus... well, this 120 volts is squared by the way... plus 2π times the frequency of 10.0 kiloohms times 3.00 times 10 to the minus 3 henries minus 2π times 10.0 times 10 to the 3 hertz times 5.00 times 10 to the minus 6 farads and this product in square brackets here has an exponent negative 1 and then this difference gets squared and this all works out to 16.0 watts.