Question
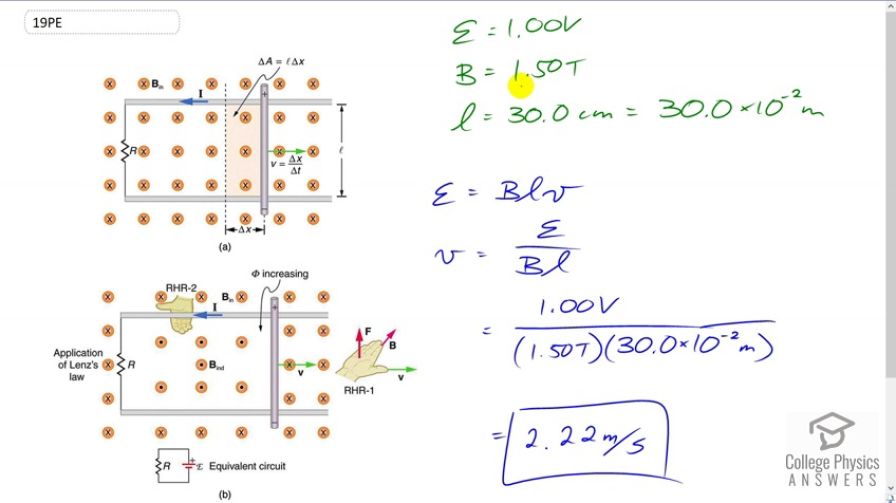
At what speed must the sliding rod in Figure 23.11 move to produce an emf of 1.00 V in a 1.50 T field, given the rod’s length is 30.0 cm?
<b>Figure 23.11</b> A motional EMF is induced between the rails when this rod moves to the right in the uniform magnetic field. (b) Lenz’s law gives the directions of the induced field and current, and the polarity of the induced emf.
Figure 23.11 A motional EMF is induced between the rails when this rod moves to the right in the uniform magnetic field. (b) Lenz’s law gives the directions of the induced field and current, and the polarity of the induced emf.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

2.22 m/s2.22 \textrm{ m/s}

Solution video

OpenStax College Physics, Chapter 23, Problem 19 (Problems & Exercises)

OpenStax College Physics, Chapter 23, Problem 19 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 23, Problem 19 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to figure out what speed this rod must move in order to have an induced EMF of one volt. Given the magnetic field strength of one and a half Tesla and a length of 30 centimeters. So, we have a formula for the EMF induced in the moving rod, assuming that the magnetic field length and velocity are all mutually perpendicular, which they are here. And, we can solve this for V by dividing both sides by B L and then switching the sides around. So, V is induced EMF divided by magnetic field strength time length. So, that's one volt divided by one and a half Tesla times 30 times ten to the minus two meters, which gives 2.22 meters per second.