Question
A research Van de Graaff generator has a 2.00-m- diameter metal sphere with a charge of 5.00 mC on it. (a) What is the potential near its surface? (b) At what distance from its center is the potential 1.00 MV? (c) An oxygen atom with three missing electrons is released near the Van de Graaff generator. What is its energy in MeV at this distance?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 45.0 MV45.0 \textrm{ MV}
  2. 45.0 m45.0 \textrm{ m}
  3. 132 MeV132 \textrm{ MeV}

Solution video

OpenStax College Physics, Chapter 19, Problem 31 (Problems & Exercises)

OpenStax College Physics, Chapter 19, Problem 31 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

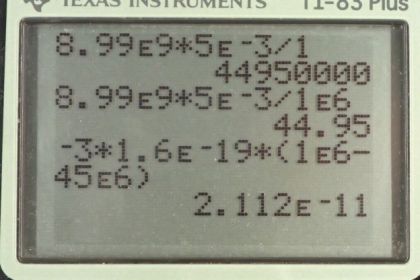
Calculator Screenshots

  • OpenStax College Physics, Chapter 19, Problem 31 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 19, Problem 31 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. The Van de Graff generator has a sphere of diameter of two meters, which means its radius is half of that, which is one meter. And so, the potential near the sphere, let's suppose that near means on the surface of the sphere. And so, we'll imagine that the sphere is like a point charge, and we'll have R is one meter in our formula for the potential due to a point charge, K Q over R. So, we have Coulomb's constant time the charge of 5 miliCoulombs, which is times ten to the minus three Coulombs, divided by one meter, giving us 45.0 megavolts as the potential down on the surface of the Van de Graff generator. And then we're asked to figure out at what distance will the potential be one megavolt. So, we can rearrange this formula by multiplying both sides by R over V, and we solve for R. So, R equals K Q over V. So, that's Coulomb's constant times 5.00 times ten to the minus three Coulombs divided by 1.00 times ten to the six volts, and that gives 45.0 meters. And then in part C, we're asked: Suppose an oxygen atom with three missing electrons, which is a clue that it has a charge of positive three times elementary charge, is released near the Van de Graff generator which will take to be at the surface of the generator. And, what will its energy at the distance found at part B, which is at a position of 45 meters. While the change in kinetic energy of this oxygen ion will be the opposite of its change in potential energy, and change in potential energy is the charge times the potential difference through which it is accelerated. And so, we have this negative times three times 1.6 times ten to the minus 19 Coulombs, so this is the charge on the oxygen ion since the three unmatched protons in the nucleus due to the three missing electrons. And then, we have this change in potential, so there's a final potential of one times ten to the six volts, because that is the potential at this position in part B, minus the initial potential it started at, which was 45.0 megavolts, or 45 times ten to the six volts. This works out to this many Joules, but the question says express your answer in electron volts, so we multiply it by one electron volt for every 1.6 times ten to the minus 19 Joules, and we end up with 132 mega electron volts of energy.

Comments

Submitted by qea on Wed, 01/04/2023 - 20:33

link

I understand that the question-maker will also suppose the metal sphere to be a point charge to solve this problem.
However, a metal sphere should only be assumed to be a point charge if the concerned distance is **sufficiently large**

if the concerned point-of-potential is near the surface of the metal sphere (charges are **on** the shere),

then without knowing the distance between the "point-of-concerned-potential" and the surface where the charges are ,
we cannot calculate the potential at that distance.

Hi qea, thank you for the insightful comment. It turns out that considering the metal sphere as a point charge is not an approximation, but rather it is exactly true so long as the distance to the point-of-potential is outside of the sphere. I think where you're coming from is when there are questions concerning a dipole, then that dipole can be approximated as a single point charge at large distances - and this approximation holds only for large distances. In this scenario of a charged conducting sphere, however, there is no approximation. The way I like to think of it is that, when close to the sphere, the charges on the near side of the sphere are responsible for a larger potential difference compared with a hypothetical point charge at the center, whereas the charges on the far side of the sphere are responsible for a smaller potential difference than the hypothetical point charge, and that these differences compensate for each other to give the same result as for a point charge at the center of the sphere. A more rigorous analysis would be to apply Gauss's Law. Hyperphysics has some pretty good articles about that which I encourage you to read. First read about the electric field due to a charged conducting sphere, and then the electric potential due to a charged conducting sphere.

All the best,
Shaun