Question
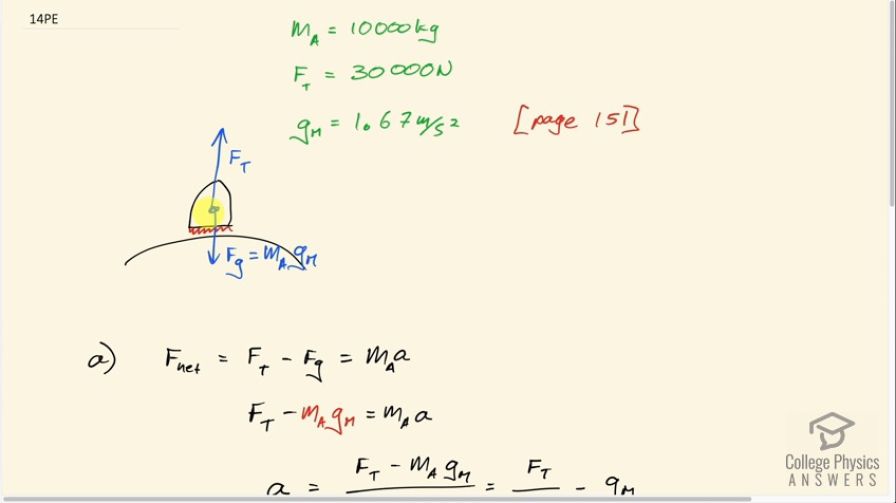
Suppose the mass of a fully loaded module in which astronauts take off from the Moon is 10,000 kg. The thrust of its engines is 30,000 N. (a) Calculate its the magnitude of acceleration in a vertical takeoff from the Moon. (b) Could it lift off from Earth? If not, why not? If it could, calculate the magnitude of its acceleration.
Final Answer
- if using the incorrect acceleration due to gravity on the moon of
- The module would not lift off from Earth.
Solution video
OpenStax College Physics for AP® Courses, Chapter 4, Problem 14 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The astronauts are in this space module and the thrust is going to result in a force upwards of 30,000 newtons. The mass of the astronauts and space module together is 10,000 kilograms. The question is, what acceleration will this module have upwards? We need to consider also the force of gravity due to the moon downwards, which is going to be the mass of the astronauts and space module multiplied by the acceleration due to gravity on the moon. On page 151, we're told that on the moon, acceleration due to gravity is about 1.67 meters per second squared. We say that the net force is the total upforce which is just that due to the thrust minus the downforce which has gravity, that equals mass times acceleration, since that's Newton's second law. Now we can replace mag m in place of Fg and then divide both sides by the mass of the astronaut and space module to solve for a. So the acceleration is the thrust minus the mass times gravitational field strength from the moon divided by mass. We can divide this m into this each term separately if we want. You don't have to do this but have written it as force of thrust divided by mass minus the acceleration due to gravity on the moon. So it's 30,000 Newton's divided by 10,000 kilograms, minus 1.67 meters per second squared, which is a positive acceleration of 1.33 meters per second squared. Since its acceleration is positive, that means it's in the direction upwards on this picture, because we've defined upwards to be positive here. So sure enough, they will be accelerating away from the moon. But if they were on Earth, the acceleration would be 30,000 students divided by 10,000 kilograms minus 9.8 meters per second squared, this being the acceleration due to gravity on the earth and that would result in acceleration of negative 6.8 meters per second squared. So if they were in the air close to the Earth, then the acceleration would be downwards towards the earth, and that means they will not escape the earth.
Comments
Gravitational acceleration of the moon is 1.625 m/s^2, not 1.67 m/s^2.
Hello Ashod, thank you for your comment. You're quite right, as confirmed on Wikipedia, and on the revised version of the textbook. I was working from a previous version of the textbook where the acceleration due to gravity was incorrectly stated as . I'll make a note of this below the final answer.
All the best,
Shaun


