Question
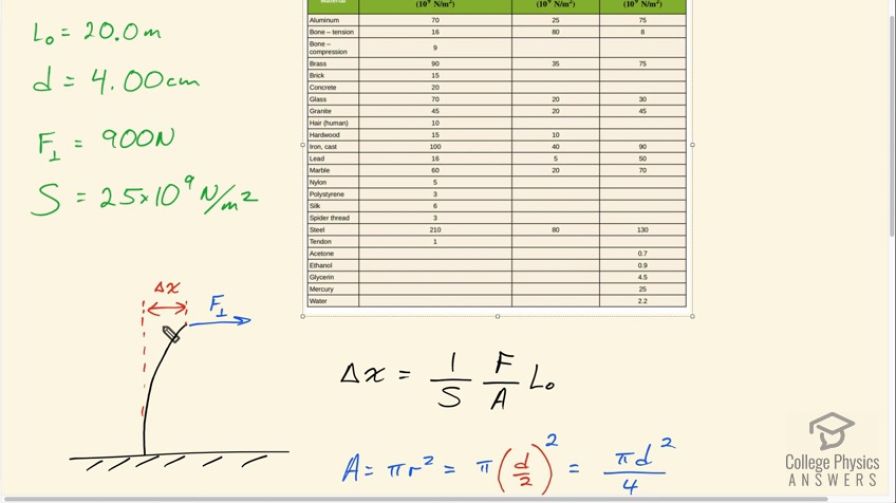
A 20.0-m tall hollow aluminum flagpole is equivalent in stiffness to a solid cylinder 4.00 cm in diameter. A strong wind bends the pole much as a horizontal force of 900 N exerted at the top would. How far to the side does the top of the pole flex?
Final Answer
Solution video
OpenStax College Physics, Chapter 5, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An aluminum flagpole that is 20 meters long is being blown by some wind that's going perpendicular to the flagpole to the side here and it's going to bend the flagpole over some distance delta x. Our job is to figure out what is that distance that the top of the flagpole moves over. This is a sheer force because the force is perpendicular to the length of the material. We need the sheer modulus and we're told that the flagpole is aluminum and so we look in here for aluminum and we go across to shear modulus, which is 25 times 10 to the 9 newtons per meter squared. The force we're told is 900 newtons and the diameter of the flagpole is equivalent to 4.00 centimeters. Here's our formula for the displacement to the side due to shear force. That's 1 over the sheer modulus times the force applied divided by the cross-sectional area times the length of the material. The area is pi r squared, but we're given the diameter and so we'll substitute diameter divided by 2 in place of radius. This works out to pi d squared over 4. When dividing by the area, we can instead multiply by its reciprocal. That's why I've written multiplied by 4 over pi d squared here. Then we plug in the numbers. The amount of the flagpole is bent over, it's going to be 1 over 25 times 10 of the 9 newtons per square meter times 4 over pi times 4 times 10 to the minus 2 meters diameter squared, times 900 newtons times 20 meters length. This works out to 0.57 millimeters. My drawing is definitely not to scale. The flagpole is going to go over probably an imperceptibly small amount in this drawing, because this is meant to be 20 meters and then this little displacement to the side is 0.57 millimeters.
Comments
I'm following this exact process and the answer is still wrong??
Hi Kaylee, have you compared what you're typing in with the calculator screenshot? Maybe that would help?
All the best,
Shaun
I have followed the steps exactly as shown and am also still getting the wrong answer. And I compared the steps to what you have shown on the calculator.


