OpenStax College Physics, Chapter 5, Problem 26 (Problems & Exercises)

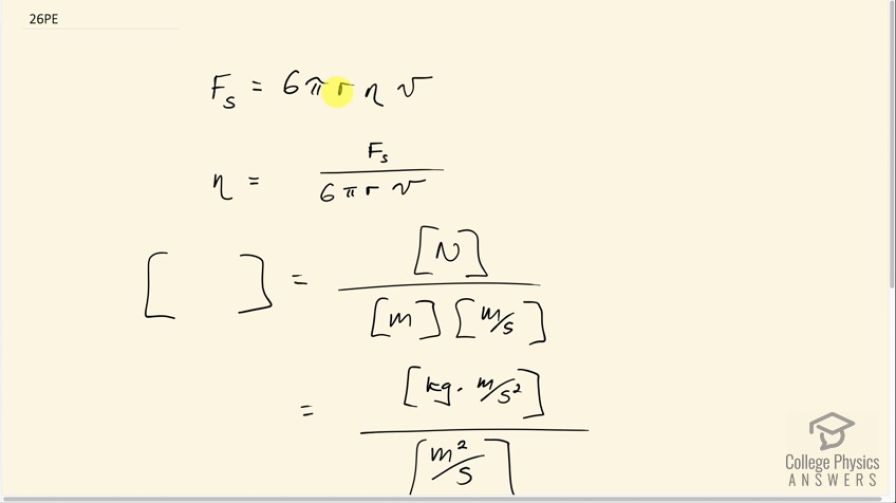
This is College Physics Answers with Shaun Dychko. We have Stoke's law which tells us that drag force on a small particle or on an object moving slowly through a fluid and it's 6 times π times the radius of the spherical object times the viscosity of the fluid that it's moving through times its speed and we are going to rearrange this to solve for the viscosity and then we'll figure out the units of viscosity by looking at the units at the right hand side here. So we divide both sides by 6πrv and we solve for η. So the units of η are the same as the units of the right hand side here so we are doing dimensional analysis and so we are writing in brackets here the units of each of these factors. So the units of force is newtons and the units of radius is meters and the units of speed is meters per second and the 6 and the π are dimensionless— they have no units, in other words. Then we can expand the newtons and write it as... based on this formula here by the way force is mass times acceleration, we are gonna write the units of newton's as kilograms times meters per second squared and then we wanna change this into something that looks like this: kilograms per meters per second. So we can do anything we want so long as we are multiplying with the number 1. So I'm gonna write this as multiply by seconds squared over seconds squared— that's the number 1— and on the top here, the seconds squared's cancel because it's a bit confusing having fractions within fractions but this is a seconds squared being multiplied by this whole numerator which contains a seconds squared denominator which cancels with this one and here we are gonna be left with just seconds in the end because seconds squared divided by seconds makes seconds to the power of 1. Okay! And then we'll multiply top and bottom by 1 over meters and then that cancels this meter away completely so in the top here now we have only kilograms and then on the bottom, we'll have this meters squared turn into meters to the power of 1 as it cancels with this meters. So we are left with kilograms per meter and per second. And there we go, we have shown the units of viscosity to be kilograms per meter per second.