Question
(a) If half of the weight of a small 1.00×103 kg1.00 \times 10^3 \textrm{ kg} utility truck is supported by its two drive wheels, what is the magnitude of the maximum acceleration it can achieve on dry concrete? (b) Will a metal cabinet lying on the wooden bed of the truck slip if it accelerates at this rate? (c) Solve both problems assuming the truck has four-wheel drive.
<b>Table 5.1</b> Coefficients of Static and Kinetic Friction
Table 5.1 Coefficients of Static and Kinetic Friction
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 4.9 m/s24.9 \textrm{ m/s}^2
  2. 4.9m/s24.9 \textrm{m/s}^2 the cabinet will not slip since the acceleration of the truck does not exceed the maximum possible acceleration of the cabinet.
  3. 9.8 m/s29.8 \textrm{ m/s}^2

Solution video

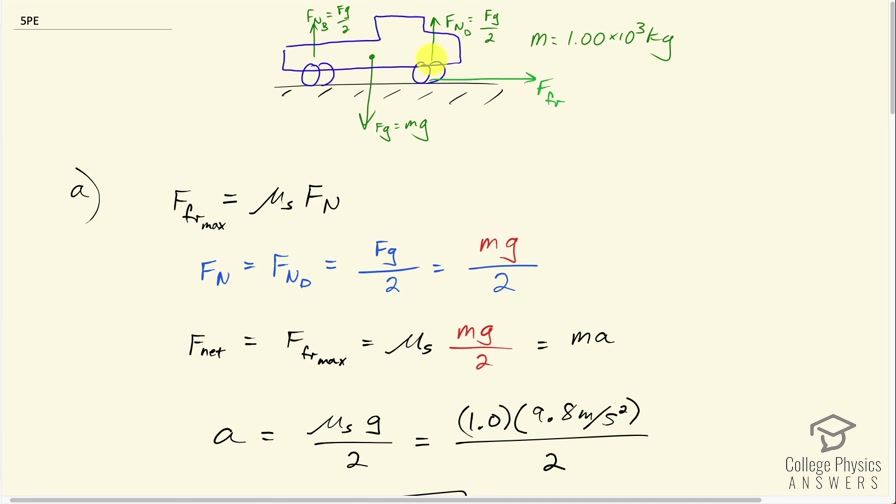
OpenStax College Physics, Chapter 5, Problem 5 (Problems & Exercises)

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 5, Problem 5 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. This is a utility truck which is two-wheel drive and we are told that half of the weight of the truck is supported by the drive wheels and so there is a force of gravity downwards equal to mass times gravitational field strength and that gravity downwards is compensated for by the total normal force upwards and the total normal force upwards has to equal the gravity downwards because the truck is not accelerating vertically. So we are told that half the weight is supported on the drive wheels and that's why this normal force has a subscript D on it for 'drive wheels' and we are dividing by 2 because half the weight is supported by these wheels. This 2 is not the number of wheels... even though there are two of the wheels, it's just coincidence that the number of wheels is 2 and this denominator is 2— this denominator 2 comes from the fact that half of the weight is supported by the drive wheels. Had there been three wheels in the front that were drive wheels... of course you will never see that but you know supposing, it was true there were three drive wheels... well, nevertheless this reaction would still be force of gravity divided by 2 because half the weight is supported by the drive wheels however many drive wheels there are... doesn't matter... it's how much weight is supported by those wheels that is important. Okay! There's also a normal force in the back wheels equal to the remainder of, you know, gravity that needs to be supported by the normal force and that's going to be F g over 2 but that's not important there, what's important is the total normal force on the drive wheels. Okay! The question in part (a) is what is the maximum acceleration of the truck? And so there's this friction force that's going to propel it forward and the friction force at its maximum will be the coefficient of static friction between the tires and the road multiplied by the normal force and this is F N D here for 'drive wheels'. And the normal force on these drive wheels is the weight of the truck—F g—divided by 2 and that is mg over 2 where the force of gravity is mass of the truck multiplied by gravitational field strength. Okay! So the net force horizontally is the friction force which is going to be at its maximum for this calculation and so that is the coefficient of static friction times mg over 2 and that's going to be mass times acceleration because that's Newton's second law and the mass will cancel out on both sides, we will divide both sides by m and we are left with acceleration after we switch the sides around acceleration on the left equals μ sg over 2 on the right so we did a switcheroo here to get to this line here— and the coefficient of static friction will be 1.0 because that's the coefficient of static friction for rubber on dry concrete— 1.0 times 9.8 meters per second squared— acceleration due to gravity— divided by 2 and that's 4.9 meters per second squared will be the acceleration of the truck when it is two-wheel drive. Okay! Part (b) asks us will the metal cabinet in the wooden flatbed of the truck slide in this scenario when the truck is accelerating at 4.90 meters per second squared? So here's a free-body diagram of the cabinet and it's a simple diagram that ignores the wheels of the truck and so on... this question is just to do with the cabinet and the surface of the flatbed... that's all that matters here. So this F N is the normal force on the cabinet, F g here is mass of the cabinet times acceleration due to gravity— notice that I sometimes call this factor acceleration due to gravity and other times I call it gravitational field strength both terms are correct... kind of depends what the context of your question is. Okay—we are going to call it acceleration due to gravity most of the time even though I think I said gravitational field strength up above. Okay! So the letters here are different than for part (a) so m here is mass of the cabinet whereas m up here was the mass of the truck but the mass of the cabinet, it's going to cancel out anyway. Alright! So the normal force upwards equals force of gravity downwards and so it is the mass of the cabinet times g because there is no vertical acceleration. And the maximum friction force is the coefficient of static friction— in this case, it's going to be the coefficient between metal and wood so this is a different coefficient of static friction than we had in part (a) so I could have put another subscript on here to say coefficient of static friction for the truck tires or something like that but just to be a bit more speedy I am just reusing the regular μ s with no other subscript, I am just saying with words what I mean here and this is the coefficient of static friction between metal and wood. So we multiply that by the normal force which is mg substituting that in here and we have the maximum friction force is also the net force horizontally and so that's going to equal the mass of the cabinet times its maximum acceleration. So we have mass of the cabinet times its maximum acceleration equals μ smg because both of these are equal to the maximum friction force and we can divide both sides by m and we get maximum acceleration of the cabinet then is the coefficient of static friction times acceleration due to gravity— and this is 0.5 for the coefficient of friction... that is metal on wood— and we multiply that by 9.80 meters per second squared and that is 4.9 meters per second squared. So because the acceleration of the truck is not more than the maximum possible acceleration for the cabinet that means the cabinet will not slip although we are right on the threshold; this is the very maximum that the cabinet can sustain for acceleration and the truck is indeed going at exactly that acceleration so this is the threshold between when it will and it will not slip but since it begins not slipping, it will continue to not slip and there we go! Part (c) says answer both these questions assuming four-wheel drive. So now the normal force on the drive wheels will equal the total weight of the truck mg and again it doesn't matter how many wheels are involved, what matters is that the drive wheels... be it 4, 6 or whatever... I mean it is common to have 6 drive wheels or you know, you can have a truck with a dually wheels in the back where there's a pair of wheels so you can have six tires driving it maybe. In any case, it doesn't matter... what matters is what is the total weight supported by the wheels that will be driving and the answer is the total weight of the truck mg. Okay! So the maximum friction force then is coefficient of static friction times the normal force on the drive wheels, which is equal to the weight mg and this maximum friction force is the net force and so it is mass of the truck times its maximum acceleration so both of these are each equal to the maximum friction force and so we can equate these two things here. Okay! And then divide both sides by the mass of the truck and we are left with maximum acceleration is coefficient of static friction between the tires and the concrete times acceleration due to gravity— and we already looked up that coefficient of static friction for rubber on dry concrete is 1.0— times 9.8 meters per second squared, which is 9.8 meters per second squared. So the four-wheel drive will cause the truck to have double the maximum acceleration so yay for four-wheel drive! Will the cabinet slip? Yes because now the truck is going to accelerate at 9.8 meters per second squared which exceeds the maximum possible acceleration for the cabinet because even though the truck is two-wheel drive vs. four-wheel drive, nothing's changed for the picture for the cabinet. As far as the cabinet's concerned, there's just a cabinet and there's a wooden flatbed and what is the maximum acceleration that the static friction force can sustain between these two objects? And we already calculated that, it was 4.9 and that's not going to change and so yes the cabinet will slip because the truck is going to accelerate faster than the cabinet possibly can. And there we go!

Comments

I don't get why in Number b, you didn't divided the g(9.81) by 2???

Thanks very much for your question, and sorry I didn't get back to it sooner. It might not be relevant to your course anymore, but hopefully is to other students!
In part a) we divided the truck weight by 2 since the front tires carry half the truck weight (the question tells us this). In part b) on the other hand, we're dealing with a metal cabinet in the truck box. The normal force applied by the truck box on the metal cabinet is the full weight of the cabinet, hence no need to divide by 2. The weight of the cabinet is being supported by only one thing, namely the truck box, whereas the weight of the truck is being supported by 2 sets of wheels, only one of which is applying static friction to the ground since we assume it's a front wheel drive truck.

Just to clarify. The question said "metal cabinet lying on the [wooden] bed of the truck." So, the coefficient in part b should be 0.5 not 0.6.

Thank you Devin.Reid, you're quite right. I made the mistake of assuming the truck box was metal. I have put a note in the Final Answer section about this.

oof. this video should be re-done. your mistake makes it too hard to follow for the answers.

Why do you use the formula for static friction? If it's accelerating (ie., moving), shouldn't it be the kinetic friction formula?

How do you say that 4.9 m/s2 is the maximum acceleration for the truck? We don't know the force that the truck is putting down with the tires. you just gave the force needed to get the truck moving, right?

Thanks for the question jdanner917. The force to accelerate the truck is due to static friction, and there's a limit to how large that static friction force can be. In part (a) we see that the force that the truck is putting down on with the tires is mg/2mg/2 on each tire since it's being pulled down by gravity, and the ground therefore pushes up on the tires with the same force since the truck isn't accelerating vertically. We know the force on the tires, in other words, but not as a number (not in newtons). That's OK, though, since the mass of the truck cancels on both sides of the equation since the friction force is the net force and we can therefore set it equal to mama. Since there are two tires driving the truck (not 4 in this case), and we're presuming the coefficient of friction of rubber on dry concrete of 1.01.0, the video shows dividing gg by 2 (since there are two tires) to arrive at 4.9 m/s^2.
Hope this helps,
Shaun

Hello michael,
Thank you for the question. It might be useful to think of this in a different way than I explained in the video. Consider that each wheel is vertically supporting the truck. This is always true, regardless of whether there is 2 wheel drive vs. 4 wheel drive. Each wheel will experience a vertical normal force from the ground. Suppose you calculated this normal force per wheel - it would be mg4\dfrac{mg}{4}, which divided the total weight of the truck, mgmg, by 4. Then, let's consider the horizontal acceleration. In part (a) only 2 of the wheels will experience a horizontal static friction force since it's two wheel drive. That force will be 2 times the force per wheel - 2×μs×mg42 \times \mu_s \times \dfrac{mg}{4}. This equals the μsmg2\mu_s \dfrac{mg}{2} shown in the video. Then, finally getting to your question, consider part (c). The horizontal friction force will be 4 times the friction force per wheel - 4×μsmg44 \times \mu_s \dfrac{mg}{4}, which is μsmg\mu_s mg. Only μsg\mu_s g is shown in the video since I skipped the algebra step of canceling mm's.
Hope this helps,
Shaun

Has the video for this problem been updated yet?

So in using metal on wood of .6. the a-max is 4.9m/s2 instead of 5.9m/s2 right? Thus, it is equal to part a (4.9m/s2) ...does that mean it does not slide?

Hi blue,
Thank you for the question (and the reminder to re-do this one...). I've added this note to the final answer to clarify: "the cabinet will not slip since the acceleration of the truck does not exceed the maximum possible acceleration of the cabinet".
All the best,
Shaun

oops I mean coefficient 0.5. (not .6)

I don't get how you relate these different values such as the maximum acceleration of the metal cabinet on the truck bed and the maximum acceleration of the truck itself. The maximum acceleration of part (a) is related to the truck and the road, but in part (b) it appears to be related to the cabinet and the truck bed. So, I don't understand how these acceleration values are directly related, or compared, to answer whether the cabinet will slip. It's difficult for me to conceptualize when I think about, for example, how the cabinet doesn't accelerate relative to the truck bed when the truck accelerates relative to the road. What even is the force that causes the cabinet to accelerate when it slips?

This video was updated on Dec. 8th, 2023