Question
Find the terminal velocity of a spherical bacterium (diameter 2.00 μm2.00 \textrm{ }\mu\textrm{m}) falling in water. You will first need to note that the drag force is equal to the weight at terminal velocity. Take the density of the bacterium to be 1.10×103 kg/m31.10 \times 10^3 \textrm{ kg/m}^3.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

2.39×10−6 m/s2.39 \times 10^{-6} \textrm{ m/s}

Solution video

OpenStax College Physics, Chapter 5, Problem 27 (Problems & Exercises)

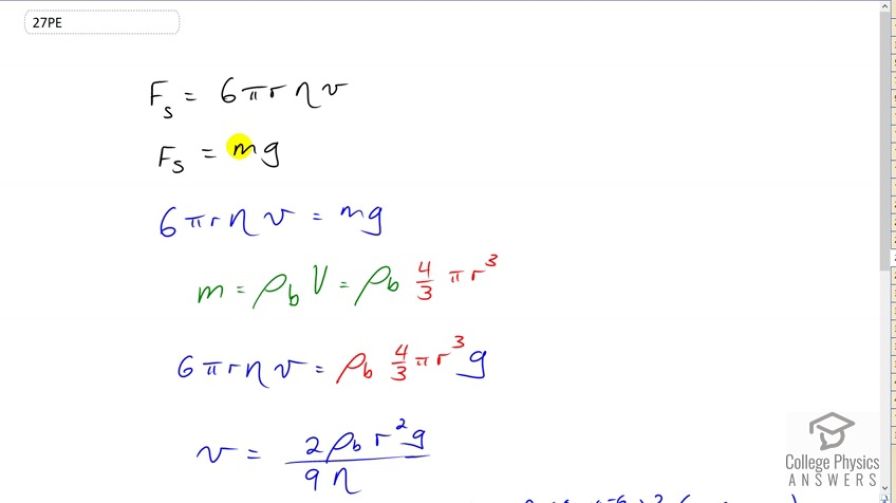
OpenStax College Physics, Chapter 5, Problem 27 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 5, Problem 27 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. This bacterium is so small that the drag force will be given by Stokes' theorem because it’s only two micro-meters in diameter, that’s why we know this formula can apply because it’s so small. So that’s six times pi times the radius of the bacterium times the viscosity of the water that it’s going through multiplied by speed. Now when it’s at terminal velocity, it means that this drag force is equal to its weight, and so we can say mg is equal to 6 pi r nu v. And the mass, we need to substitute for that, is going to be the density of the bacterium multiplied by its volume. So that’s the density of the bacterium times four thirds pi r cubed, volume of the sphere, and so we rewrite this formula in blue here but make a substitution for mass, and we have 6 pi r nu v equals density of bacterium times four thirds pi r cubed times g. Then we solve this for v by dividing both sides by 6 pi r nu and this works out to two times density of bacterium times r squared times g over nine times viscosity of water. So this is two times 1.1 times ten to the three kilograms per cubic meter, that’s the density of the bacterium, times by the radius which is two micro-meters divided by two, this was the diameter we were given, so we have to divide by two to get the radius, and then square that result, times 9.8 divided by nine times 1.002 times ten to the minus three pascal seconds, which is the viscosity of water given in Table 12.1, water at 20 degree Celsius, I’m just assuming that that’s the temperature this water’s going to be. And this will work out to 2.39 times ten to the minus six meters per second.

Comments

Where did the formula for mass come from? m=pbV=pb4/3pir^3?

Hi georgeh, thanks for the question. Density is defined as mass per volume, which is written as ρ=mV\rho = \dfrac{m}{V}. This can be rearranged to solve for mass by multiplying both sides by volume. Doing this makes m=ρVm = \rho V. The ρ\rho in the video has a subscript b just as a label to say that it's the density of the bacterium. Then, since the bacterium is assumed to be a sphere, the volume is substituted with the formula for the volume of a sphere, which is 43πr3\dfrac{4}{3}\pi r^3. In the end this makes m=ρb43πr3m = \rho_b \dfrac{4}{3}\pi r^3.
Hope this helps!
All the best,
Shaun

im confused as to where the '2pb' came from in the second last step for v

Are you at 1:15 in the video? I think the calculation you might be wondering about is where the 29\dfrac{2}{9} comes from? That's the result of 43\dfrac{4}{3} divided by 66.
Hope this helps,
Shaun

Thank you for your help on this question. I just needed a nudge and got the answer which was confirmed by yours. Any thoughts on what the threshold is for moving from the standard F(D) equation to the Stokes equation? The book just says "very small" and if you use the standard equation, you have an unknown for C in addition to v which stumped me for about 20 minutes...

Also quite distressing that the text assumes we know what viscosity is about when it isn't covered until chapter 12 and this question is in chapter 5 :)

Thanks for your time and assistance.