Question
A camera with a 50.0 mm focal length lens is being used to photograph a person standing 3.00 m away. (a) How far from the lens must the film be? (b) If the film is 36.0 mm high, what fraction of a 1.75 m tall person will fit on it? (c) Discuss how reasonable this seems, based on your experience in taking or posing for photographs.
Final Answer
- 100% of the image will fit on the film since the image size is less than the film size.
- Yes, this is reasonable since it's normally possible to take a photo of an entire person from 3.0m away.
Solution video
OpenStax College Physics, Chapter 25, Problem 44 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
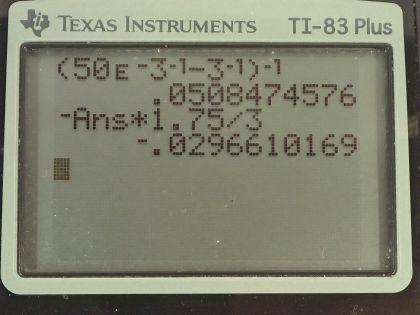
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A camera with a 50.0 millimeter focal length is being used to photograph a person who is standing 3.00 meters away. So the person is the object and so this 3.00 meters gets labeled d o for object distance. In order to have consistent units in our thin lens equation, let's change the focal length into meters as well so that's 50.0 times 10 to the minus 3 meters. We want to know where should the film in the camera be placed, how far from the lens and that will be the image distance, in other words and so we are gonna solve this thin lens equation for d i. Let's subtract 1 over the object distance from both sides and so we have 1 over image distance on the left equals 1 over focal length minus 1 over object distance. This 1 over focal length can be written instead as f to the power of negative 1 because this exponent negative 1 means take the reciprocal and then minus object distance to the power of negative 1 and I like using this negative 1 exponent because there's a key on the calculator that is just negative 1 exponent. And then we take both sides of this equation to the power of negative 1 to solve for d i and so we have d i on the left— image distance— and on the right hand side, we have all these brackets to the exponent negative 1. So then we plug in numbers so that's 50.0 times 10 to the minus 3 meters—focal length— to the power of negative 1 minus 1 over 3.00 meters—I am just speaking in this in terms of this here, which is the same as 3.00 meters to the power of negative 1, take that difference and then the result of that is raised to the exponent negative 1 and you get 0.0508475 meters and this... it can be written as 5.08 centimeters so we can multiply this by 100 centimeters for every meter. Okay! So the film and the camera should be 5.08 centimeters away from the lens. Part (b) is asking if the film is 36.0 millimeters high, what fraction of a 1.75 meter tall person will fit on it? So h o is 1.75 meters— the size of the object, the height of the person in other words. We want to know what is the image height then and compare that with the size of the film. So magnification is image height divided by object height and that also equals negative of image distance over object distance and so we know the image and object distances now and the object height and so we can solve this for h i by multiplying both sides by h o. So the height of the image of this person on the film then is going to be negative of the image distance times the object height divided by the object distance. So that's negative of 0.0508475 meters— that we found in part (a)— multiplied by 1.75 meters— height of the person— divided by 3.00 meters—distance between the lens and the person— and that gives negative 0.029661 meters, which we convert into centimeters and that is negative 2.96 centimeters. Now the height of the film is 36.0 millimeters and in order to compare this number with the image height, let's make the units the same so we will convert this into centimeters by multiplying by 1 centimeter for every 10 millimeters and we get 3.60 centimeters for the height of the film. This negative sign just means that the image is going to be flipped over compared to the object and so we are just comparing the magnitudes of these two heights and so the magnitude of the image is 2.96 centimeters which is less than the magnitude of the film height, which means the entire image will fit on the film... there's lots of room to spare even. And so yes, this is reasonable because it's normally possible to take a photo of an entire person from 3.0 meters away.