OpenStax College Physics, Chapter 25, Problem 23 (Problems & Exercises)

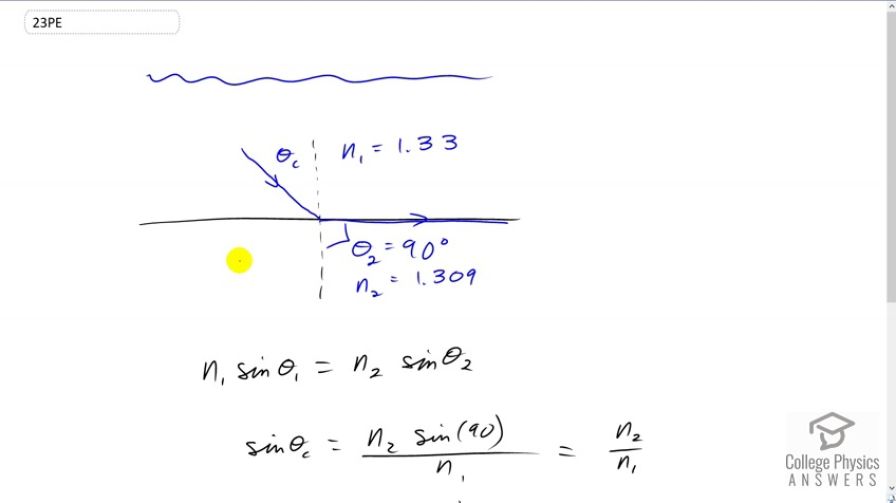
This is College Physics Answers with Shaun Dychko. We want to know at what minimum angle will we get total internal reflection at the interface between water and ice. So it's water here, and ice down below here. And, total internal reflection, it just begins to happen at this critical angle. Strictly speaking, critical angle means the angle of refraction is 90 degrees parallel to the interface, and it's just beyond that that you get total internal reflection. So this represents basically the border and we'll call that the minimum angle such that you get this total internal reflection. Snell's law says that the initial index of refraction times sine of the angle of incidence — which is the critical angle in this case — equals the second index of refraction multiplied by sine of the angle of refraction. And the angle of refraction is 90 degrees, so that's theta two. And we're gonna be solving for theta one, and we're gonna call it theta c, critical angle. Let's divide both sides by n one here, and we have sine of the critical angle then is the index of refraction of the second medium, which is ice, times sine of the angle of refraction, which is 90 degrees, and divide that by the index of refraction of the initial medium, which is water. And sine of 90 is one, and so we'll just say, n two over n one here. And so, the critical angle is the inverse sine of the index of refraction of ice divided by the index of refraction of water. So that's inverse sine of 1.309 divided by 1.333, which gives an angle of 79.11 degrees.