Question
In Example 25.7, the magnification of a book held 7.50 cm from a 10.0 cm focal length lens was found to be 3.00. (a) Find the magnification for the book when it is held 8.50 cm from the magnifier. (b) Do the same for when it is held 9.50 cm from the magnifier. (c) Comment on the trend in m as the object distance increases as in these two calculations.
Final Answer
- The magnification increases as the object distance gets closer to the focal length.
Solution video
OpenStax College Physics, Chapter 25, Problem 49 (Problems & Exercises)
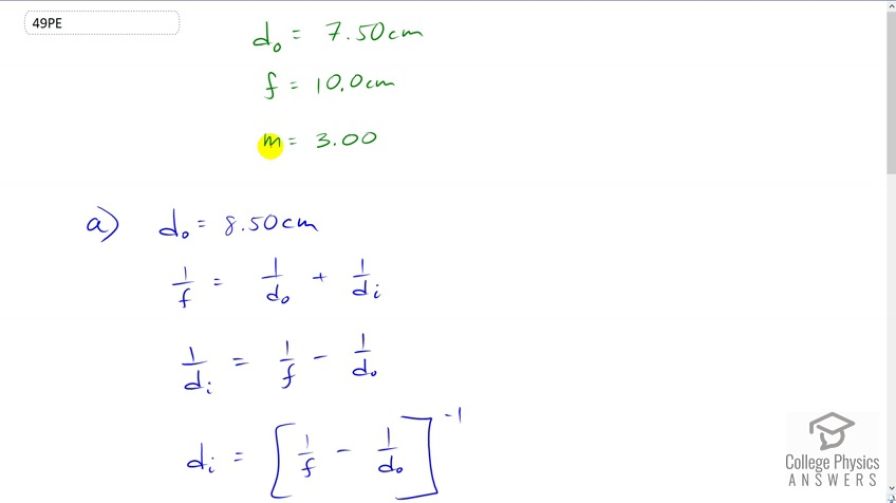
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A book is held seven and a half centimeters in front of a lens which has focal length of ten centimeters and the magnification of the image we are told is three times. So what if the book was held at 8.5 centimeters instead of 7.5? So the object distance would then be 8.5. And to figure out the magnification, we’ll take the negative of the image distance divided by the object distance. But we don't know what the image distance is, and so this work here with the lens equation is done in order to figure out image distance in terms of focal length and object distance. So one over f equals one over object distance plus one over image distance and we can solve this for one over di by subtracting one over object distance from both sides and then switching the sides around and you get one over image distance is one over focal length minus one over object distance and then we raised both sides to the exponent negative one and then left we get image distance and on the right we get one over f minus one over d naught all to the power negative one. So then this is something we can substitute in place of image distance in our magnification formula which we did here in red. So the magnification then is one over focal length minus one over object distance all to the negative one divided by object distance with a negative in front of it all. Let's write this difference as a single fraction. And to do that, we’ll multiply the top and bottom of this by object distance and then multiply top and bottom of this by focal length. We're multiplying by one in other words, which is always okay because multiplying by one doesn't change a value it just changes the way it looks. And we're going to have object distance time focus length as a common denominator and we'll have do minus f on top divided by do f on the bottom multiplied by those two are multiplied together in the bottom and then I took this one over do and then I wrote it in front of this bracket. Now this is all to the exponent negative one. So that means flip this fraction and that's what we've done here. So this is object distance times focal length over object distance minus focal length and exponent positive one there, if you like and then the object distance cancels and we left with magnification is the negative of focal length divided by object distance minus focal length. So this is a formula that we can use for answering all of the questions. So for part A, we're told that the object distance is 8.5 centimeters. So we plug that in as well as plugging in ten centimeters for focal length in both places and we get 6.67. Then if the object distance is 9.5 centimeters in part B, we have the magnification of 20 times and we can see that the magnification increases as the object distance approaches the focal point and at the focal point the image would be at infinity.
