Question
a) Find the ratio of the electrostatic to gravitational force between two electrons. (b) What is this ratio for two protons? (c) Why is the ratio different for electrons and protons?
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. 4.16×10424.16 \times 10^{42}
  2. 1.24×10361.24 \times 10^{36}
  3. The ratio of electrostatic force to the gravitational force for the electrons and protons is different since their masses are different.

Solution video

OpenStax College Physics, Chapter 18, Problem 21 (Problems & Exercises)

OpenStax College Physics, Chapter 18, Problem 21 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

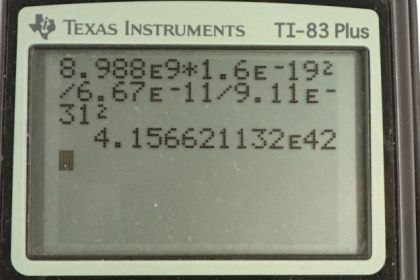
Calculator Screenshots

  • OpenStax College Physics, Chapter 18, Problem 21 (PE) calculator screenshot 1
  • OpenStax College Physics, Chapter 18, Problem 21 (PE) calculator screenshot 2
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to find the ratio of the electrostatic force to the gravitational force between two electrons and then do it again for between two protons. So the electrostatic force is Coulomb's constant times the two charges, both of which are the elementary charge and so we square them, square the elementary charge, and divide by the distance between the two charges, and the gravitational force is the gravitational constant times the mass of each electron multiplied together, divided by the distance between them squared. The ratio of these two forces is going to be the electrostatic force divided by the gravitational force. Now instead of dividing a fraction by a fraction, I'm going to multiply by the reciprocal of this fraction, so multiplying by r squared over g m e squared. This works out to k q e squared over G m e squared and the r squareds cancel. Then we substitute in numbers and we have the Coulomb's constant times the elementary charge squared, divided by the gravitational constant, times the mass of an electron squared. We get 4.16 times ten to the forty-two which is a very massive number. This means electrostatic force is way bigger than the gravitational force for electrons. Now when it comes to protons, the expression is basically going to be the same but we'll have mass of a proton down here instead of mass of an electron. So we substitute in all the same numbers as before but now the mass of electron which was 9.11 times ten to the minus thirty-one kilograms, is replaced instead with 1.67 times ten to the minus twenty-seven kilograms, mass of a proton. This works out to 1.24 times ten to the thirty-six is the ratio of the electrostatic force to the gravitational force for protons. The reason these ratios are different is because the masses are different.

Comments

You divided the gravitational constant by the mass of the electron, instead of multiplying

Hi Devin,
Thank you for the comment. I think you're looking at the first calculator screenshot? I see what you mean - there's a "divide by the mass of the electron squared" following the gravitational constant. There isn't a mistake however - there's an issue of personal preference here about how to manage multiple factors in the denominator of a fraction. I'm guessing that your approach, which is totally fine, is to enclose the denominator in brackets, in which case you would need to see a multiply sign between the gravitational constant and the electron mass. My approach (which is no better, and in your case more confusing as it turns out, but I like it since there are fewer button pushes) is to not put brackets around the denominator. Without the brackets, since the calculator works from left to right, each division is dividing the result of everything before it. The division by the electron mass is dividing the result of the numerator after it has been divided by the gravitational constant. The electron mass is dividing the result of everything before it, not dividing the gravitational constant alone.
Hope this helps,
Shaun