Question
Two point charges are brought closer together, increasing the force between them by a factor of 25. By what factor was their separation decreased?
Question by OpenStax is licensed under CC BY 4.0
Final Answer

Their separation was decreased by a factor of 15\dfrac{1}{5}.

Solution video

OpenStax College Physics, Chapter 18, Problem 13 (Problems & Exercises)

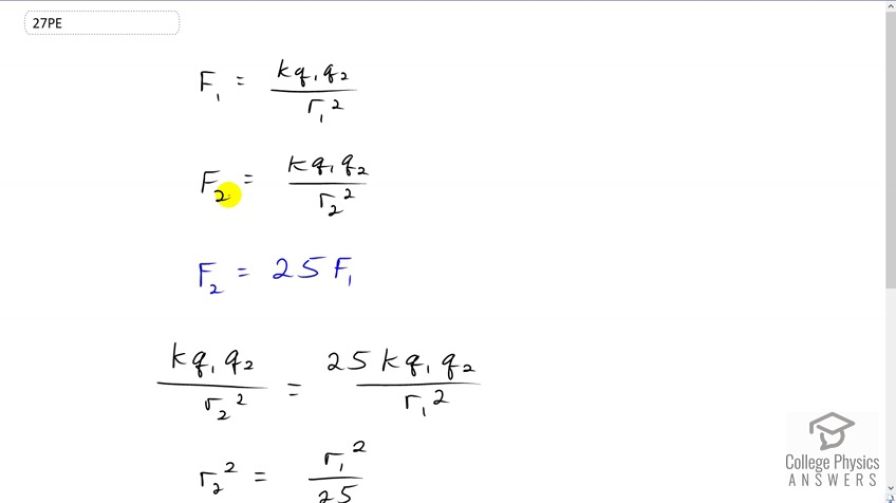
OpenStax College Physics, Chapter 18, Problem 13 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right
Video Transcript
This is College Physics Answers with Shaun Dychko. The force between two charges in the first case is kq1q2 over r1 squared. And in the second case, we're told that the charges are the same but the distance between them changes and so we have a subscript two on the r here instead. And we're told that the force in the second case is 25 times the force in the first case. So we can say F2 is 25 times F1. And we have a bunch of common factors that we can cancel divide both sides by kq1q2. Then we have one over r2 squared equals 25 over r1 squared. And we can flip both sides by raising them both to the exponent negative one or take the reciprocal of both sides in other words. And we get r2 squared is r1 squared over 25. Then take the square root of both sides and you get r2 is r1 over five. So that means the separation was decreased by a factor of one fifth.

Comments

In my homework system, the correct answer was actually 5/1 or 5. I'm not sure why the discrepancy.

I think you're right Nikki although the wording gets tricky and it's hard to know exactly what they're asking or how to answer-r2 is 1/5 of r1 or in other words it takes 5 r2's to equal 1 r1. That would mean it's decreases to 1/5 it's original value but that's not the same is as being decreased by a factor of 1/5. To put actual numbers on it if r1 was 5, r2 would be 1. But the way this is answered if r1 was 5, r2 would be decreased by 1/5 that amount (1/5 of 5 is 1)and that means r2 would be (5-1) 4 and that's not right.

Hi Elizabeth, thanks again for your comment. This issue here hinges on the meaning of "decreases by a factor of..." I take the word factor to mean a number that multiplies by something else. From this point of view a factor that reduces something must be less than one, so the factor should be 15\dfrac{1}{5}, not 55. Alternatively, it's definitely possible to see usages of the phrase "decreases by a factor of 5" with the intended meaning to divide by 5 on account of the word decreases... it really depends on the author. Definitely confusing!
All the best,
Shaun