Question
(a) What is the electric field 5.00 m from the center of the terminal of a Van de Graaff with a 3.00 mC charge, noting that the field is equivalent to that of a point charge at the center of the terminal? (b) At this distance, what force does the field exert on a charge on the Van de Graaff's belt?
Final Answer
Solution video
OpenStax College Physics, Chapter 18, Problem 51 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
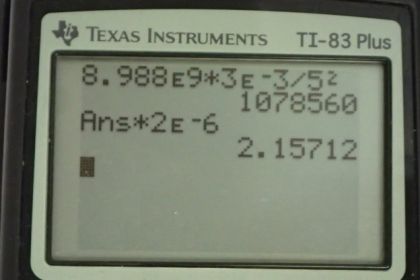
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We're going to be five meters away from this terminal of the Van de Graaf generator and there's going to be a charge of three milli Coulombs on the terminal, which is three times ten to the minus three Coulombs. And in part b, we'll use this second charge of two micro Coulombs to calculate the force that the charge will experience. So, first of all, the electric field due to the terminal of the Van de Graaf generator is kq1 over r squared. So that's 8.988 times ten to the nine Newton meter squared per Coulombs squared times three times ten to the minus three Coulombs divided by five meters squared giving an electric field of 1.08 times ten to the six newtons per Coulomb. And then the force to that electric field will exert on a two micro Coulomb charge, put there is going to be the electric field times the charge. So that's 1.0786 times ten to the six newtons per Coulomb using an unrounded number for the electric field in order to avoid intermediate rounding here. And then multiply it by two times ten to the minus six Coulombs to get a force of 2.16 newtons.