Question
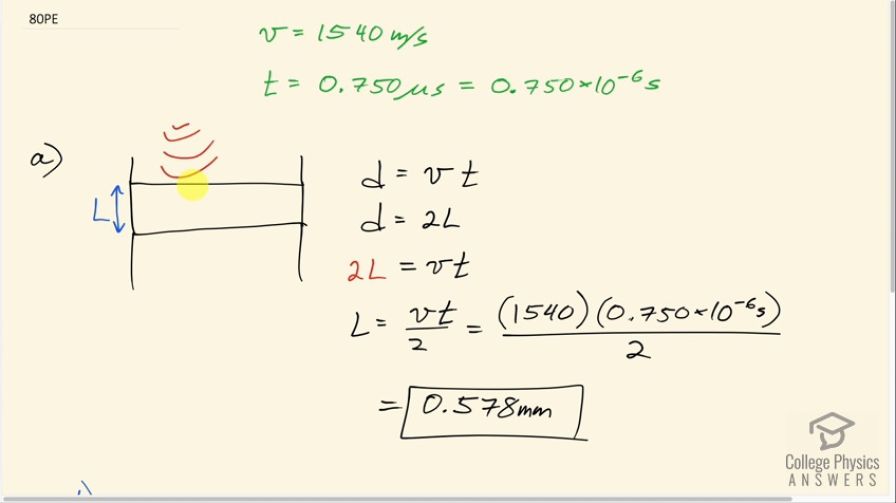
(a) How far apart are two layers of tissue that produce echoes having round-trip times (used to measure distances) that differ by ? (b) What minimum frequency must the ultrasound have to see detail this small?
Final Answer
Solution video
OpenStax College Physics, Chapter 17, Problem 80 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We imagine that some ultrasound is coming from up above say and it's gonna reflect off this first layer of tissue and then it will reflect off this second layer of tissue down here and then the time difference between when these reflections are detected is 0.750 microseconds and this time difference results from this time it takes the sound to go down this length between the layers of tissue and then back up again. So it crosses this distance twice and that accounts for the different times that the reflections are detected. Okay! So the speed of sound in tissue is 1540 meters per second and so we know that the total distance that this second sound wave has traveled is going to be the speed times the total time but this distance is 2 times the distance between the layers of tissue so we can substitute 2L in place of d here and then divide both sides by 2 and we get that the length between tissues is vt over 2. So that's 1540 meters per second times 0.750 times 10 to the minus 6 seconds divided by 2 which is 0.578 millimeters. so that's the distance between the layers of tissue. In part (b), we are asked what minimum frequency of ultrasound is needed to observe this size of a distance? So you know the wave equation says that v equals the frequency times wavelength and we are gonna assume that this is going be the wavelength because that's the maximum wavelength that's possible in which case you get the minimum frequency needed. So we divide both sides by λ and then the frequency is gonna be the wave speed divided by its wavelength. So that's 1540 meters per second divided by the answer to part (a) and that's 2.67 megahertz is the minimum frequency needed to observe this amount of separation between layers of tissue.
