OpenStax College Physics, Chapter 17, Problem 28 (Problems & Exercises)

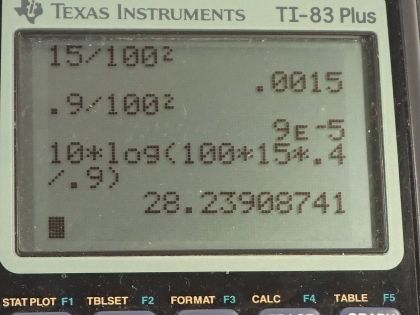
This is College Physics Answers with Shaun Dychko. In this question we want to know by how many decibels is the sound level increased due to using a stethoscope? So we are told that the area of this end of the stethoscope that touches a patient's chest is 15.0 square centimeters and the area of the ear into which that sound will be concentrated is 0.900 square centimeters and the intensity at this surface of this stethoscope is 100 times the intensity that would be emitted by the patient's chest without the stethoscope. So anything labeled with a subscript 1 is no stethoscope used at all and the subscript 2 indicates this position here at the... I don't know what you call this but the thing that touches the patient's body is this surface here I give it a subscript s as well for the area and it's intensity number 2 and it's going to be 100 the intensity without the stethoscope intensity 1 because the power will be multiplied by 100 times we are told and well at least that's the interpretation when it says that the sound is transmitted 100 times as effectively is to say that the power will increase by 100 times and now when we are comparing equal areas here with this stethoscope in this area or without the stethoscope in that same area. So anyway the I 2 is 100 times the I 1. Okay! So the intensity 2 is the power received by this stethoscope's surface divided by the stethoscope area and we can solve for P 2 and say it's the stethoscope area times I 2 by multiplying both sides by A s and then I 2 is 100 times I 1 so we have expressed P 2 in terms of I 1 now by substituting 100 I 1 in place of I 2 which we do here. Then we look at this position at the ears and the power transmitted to the ears is gonna be P 3 and it will be the efficiency multiplied by P 2 So it's the power that is transmitted through these cables or through these tubes and P 3 is Eff times P 2 and I 3 is P 3 multiplied by the area of the ears and P 3 we can make a substitution as Eff times P 2 and then down here, we go a bit further and replace P 2 with area of the stethoscope surface here times 100 times I 1 and now we have a ratio of the intensity at the ears with the stethoscope that's I 3 divided by the intensity with no stethoscope at all after dividing both sides by I 1 here or multiply by 1 over I 1. Okay... good because now we can talk about the difference in the sound levels and the sound level in the case with at the ears with the stethoscope β 3 is 10 times logarithm of I 3 over this reference intensity I naught minus 10 times the logarithm of I 1 over I naught. And when you take the difference between two logarithms, you can instead take the logarithm of the first argument divided by the second argument and so I factored out the 10 and then multiplying by logarithm of I 3 over I naught divided by I 1 over I naught but instead of dividing a fraction by a fraction, I'm multiplying by the reciprocal of the bottom fraction so let's take the reciprocal of this and multiply by it. So we multiply by I naught over I 1 the I naught's cancel and we have 10 times logarithm of I 3 over I 1. Now all this work we did up here told us what I 3 over I 1 is in terms of the areas and the efficiency in this factor 100. So then we substitute all that in place of I 3 over I 1 and so we have the increase in the sound level will be 10 times logarithm of 100 times 15.0 square centimeters times 0.400—efficiency—divided by 0.900 square centimeters and it's okay to use centimeters squared here instead of the meters squared; I just convert it to meters squared out of habit. Usually, it's the best thing to do but in this case since we are dividing these areas, the only important thing is that they have the same units and those units will cancel and it's just more convenient to write 15.0 square centimeters divided by 0.900 square centimeters than it is to write these things. Okay! All this works out to 28.2 decibels. So that's the increase in the sound level we expect by using a stethoscope compared to no stethoscope at all.