OpenStax College Physics, Chapter 34, Problem 6 (Problems & Exercises)

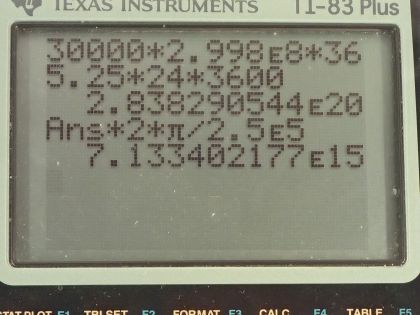
This is College Physics Answers with Shaun Dychko. We suppose that our Solar System, which is this red sun that I have drawn here is 30,000 light years from the center of the Milky Way galaxy and we have got a big Black Hole here at the center of the galaxy; we want to know how long does it take for this Solar System to do one complete orbit around the center of the galaxy assuming that it's moving at a tangental velocity of 250 kilometers per second? Let's convert these light year units into meters so we multiply by 2.998 times 10 to the 8 meters per second for every l— l represents the speed of light here, it could be written as c another way to write ly, or light years, would be c.y; you never see that but you know that's what it means anyhow— and then we have to convert these year units into seconds by multiplying by 365.25 days per year and then multiply by 24 hours per day and then 3600 seconds per hour and we have 2.838 times 10 to the 20 meters. And then the speed multiplying by 1000 meters per kilometer is 2.50 times 10 to the 5 meters per second. So the time to do one complete orbit is the distance traveled divided by the speed and the distance traveled is the circumference of the circle which has the formula 2π times its radius. So we have 2π times this distance from the center of the galaxy to the Solar System divided by the speed and that is 7.1334 times 10 to the 15 seconds, which I convert back into years because it's a little easier to understand years instead of such a big number of seconds. So we multiply by 1 hour for every 3600 seconds and then 1 day per 24 hours and then 1 year for every 365.25 days and we have 2.3 times 10 to the 8 years. So every billion years, the Sun goes around the center of the Milky Way galaxy about 5 times.