OpenStax College Physics, Chapter 34, Problem 18 (Problems & Exercises)

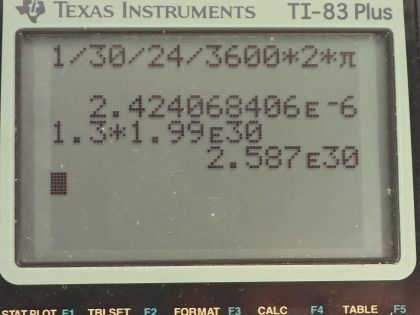
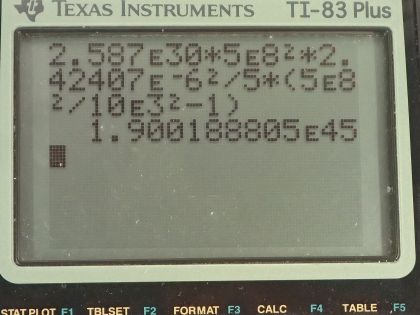
This is College Physics Answers with Shaun Dychko. A star that has 1.3 solar masses collapses after a Supernova forming a neutron star and it has an initial angular velocity of 1 revolution every 30 days which I then convert into radians per second and it has an initial radius of 5.0 times 10 to the 5 kilometers and then has a final radius after it collapses of only 10.0 kilometers and these are both converted into meters and the solar masses are multiplied by the number of kilograms per solar mass— this is the mass of the Sun by the way. So we know that angular momentum is conserved and so we have an expression for that: it's the moment of inertia of this sphere multiplied by its angular velocity and the kinetic energy though is not conserved, it's going to gain kinetic energy and let's find out how much it gains. So the expression for kinetic energy is one-half times moment of inertia times angular velocity squared. So the change in kinetic energy will be its final kinetic energy minus its initial kinetic energy. So that is one-half times its final moment of inertia times its final angular velocity squared minus one-half times initial moment of inertia times initial angular velocity squared. The moment of inertia for a sphere, which we look up in chapter 10 is 2 times the mass of the sphere times its radius squared divided by 5— that's for a solid sphere which this is. So we substitute that expression in for each moment of inertia factor and putting final radius in this term and putting initial radius in this term and then we cancel the 2's here and factor out the m over 5 from both terms so we have m over 5 times final radius squared times final angular velocity squared minus initial radius squared times initial angular velocity squared— this is the change in kinetic energy. So we are given the initial angular velocity— it's 2.42407 times 10 to the minus 6 radians per second— and we need to figure out what is the final angular velocity and we need to use conservation of angular momentum to do that. So the final moment of inertia times the final angular velocity equals the initial moment of inertia times the initial angular velocity so we can divide both sides by I f to solve for ω f. And then we substitute expressions for these moments of inertia here so we have 2m times initial radius squared over 5 substituted for initial moment of inertia times the initial angular velocity and then dividing by this fraction, I am going to instead write it as multiplying by its reciprocal since that's a bit cleaner so I am going to multiply by 5 over 2mr f squared and the 2's, the 5's and the m's cancel and so our final angular velocity then is initial radius squared times initial angular velocity divided by final radius squared so we can substitute this in place of ω f here So change in kinetic energy then is m over 5 times r f squared times r i squaredω i over r f squared all squared because this is a substitution only for ω f and ω f itself is squared in this formula here so that square remains minus r i squared times ω i squared and squaring all the factors in this bracket then gives us r i to the power of 4 times ω i squared divided by r f squared because it's r f to the power of 4 in the denominator multiplied by r f squared leaving us with r f squared in the end in the denominator and this is minus r i squaredω i squared. Now r i squaredω i squared is a common factor among these two terms and so we factor that out so we divide both terms by r i squaredω i squared and then write that factor outside the brackets and we have this expression here and then we can substitute in some numbers. So the mass is 2.587 times 10 to the 30 kilograms times an initial radius of 5.0 times 10 to the 8 meters squared times its initial angular velocity squared all over 5 times the initial radius squared divided by the final radius squared minus 1 and that's a change in kinetic energy of 1.9 times 10 to the 45 joules. And the question also asks where does this kinetic energy come from? And it comes from a loss in gravitational potential energy because it's so much smaller now and and these particles that were on the edge of the star so far away—5.0 times 10 to the 8 meters away from the center— are now only 10.0 times 10 to the 3 meters from the center so they have gotten closer. So this loss in gravitational potential energy has been converted into a gain in rotational kinetic energy.