OpenStax College Physics, Chapter 34, Problem 16 (Problems & Exercises)

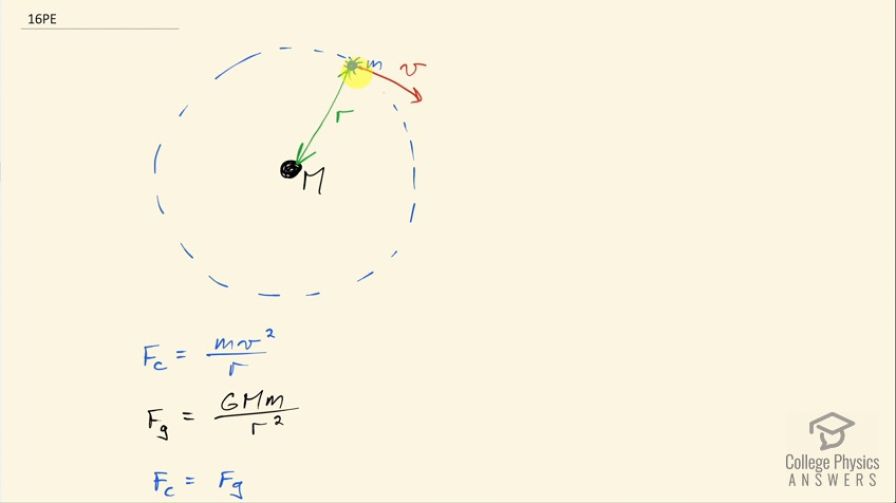
This is College Physics Answers with Shaun Dychko. We are going to show that the velocity of a star orbiting the center of its galaxy is inversely proportional to the 1 over the square root of this distance from the center to the star. So the centripetal force being provided by the center is mv squared over r— this is our centripetal force formula for the force that's needed toward the center for an object going in a circle— and this force is being provided by gravity and so we can also say that the centripetal force is gravitational constant times the mass of the galaxy times the mass of the star m over the distance between the center and the star squared. We are assuming that the galaxies mass is all concentrated in a point in the center which is roughly true because a piece of mass that's over here and a piece of mass that's over here will be pulling a bit to the one side and then a bit to the other and the net pull will be towards the center. Okay! So the centripetal force is provided by the gravitational force and so we can say mv squared over r is gravitational constant times mass of the galaxy times mass of the star over r squared. And we can multiply both sides by r over m and we get v squared then is GM over r and then take the square root of both sides and you get the velocity of the star then is the square root of gravitational constant times mass of the galaxy divided by distance from the center of the galaxy to the star and this is to say that v is proportional to 1 over the square root of r which is what we wanted to show because this G and M are just constants and so we have shown that v is proportional to 1 over square root r.