Question
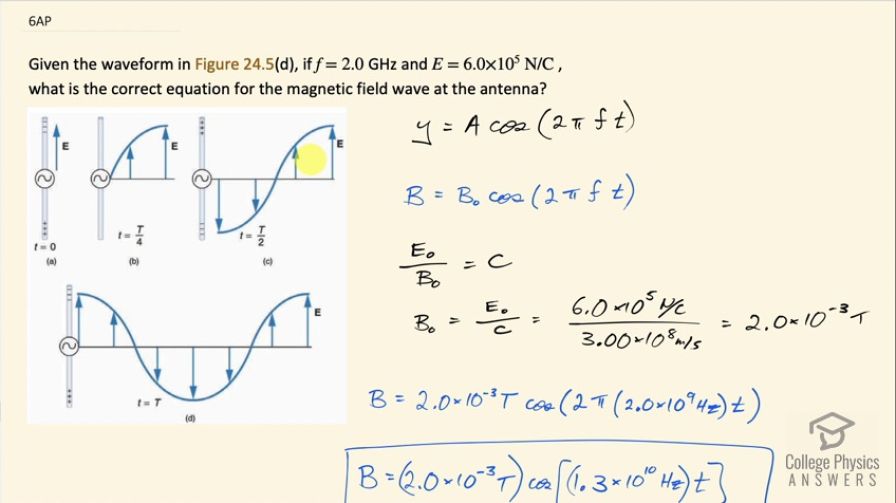
Given the waveform in Figure 24.5(d), if and what is the correct equation for the magnetic field wave at the antenna?
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 24, Problem 6 (Test Prep for AP® Courses)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. At time 0, we have an electric field at its maximum and then it propagates out in this sinusoidal form and then after one complete period at this position of the antenna, it's again at its peak and so that means this is, you know, a period when you have a return to its original state so maximum up at time 0 and maximum up at time equal to 1 period. Now we are meant to find the equation for the magnetic field and so the magnetic field is perpendicular to the electric field and its intensity is mirroring that of the electric field so when the electric field has a peak, the magnetic field also has a peak. So the equation will have the exact same phase as the electric field, which is to say in our equation for a cosine function, there's no need for a phase shift... there's no need for plus Φ here— that's not necessary— because the phase of the magnetic field would be the same as that of the electric field and the electric field is at its maximum at time 0. Okay! So the general form for a cos function then you know with a phase shift of zero is amplitude times cos of 2π times the frequency of the function multiplied by time. So we are given frequency here— 2.0 gigahertz— and the frequency for the magnetic field would be the same as that of the electric field since they are moving together at the same frequency and so we need to figure out what is this peak magnetic field— it will be a different number than the peak electric field. So we have that the ratio of electric field to magnetic field is the speed of light and in our formula in the textbook, they don't have the peak here but you could say the same for the peak ratio will still also be the speed of light and we can solve for B naught by multiplying both sides by B naught over c and then switch the sides around and we have the peak magnetic field is the peak electric field divided by speed of light. So that's 6.0 times 10 to the 5 newtons per coulomb divided by 3.00 times 10 to the 8 meters per second and that's 2.0 times 10 to the minus 3 tesla. So I substitute that in and then we also plug in this 2.0 times 10 to the 9 hertz for the frequency for f and so we multiply that by 2π and we get our final formula: the magnetic field then is 2.0 times 10 to the minus 3 tesla times cos of 1.3 times 10 to the 10 hertz times time.
