Question
Suppose the maximum safe intensity of microwaves for human exposure is taken to be . (a) If a radar unit leaks 10.0 W of microwaves (other than those sent by its antenna) uniformly in all directions, how far away must you be to be exposed to an intensity considered to be safe? Assume that the power spreads uniformly over the area of a sphere with no complications from absorption or reflection. (b) What is the maximum electric field strength at the safe intensity? (Note that early radar units leaked more than modern ones do. This caused identifiable health problems, such as cataracts, for people who worked near them.)
Final Answer
Solution video
OpenStax College Physics for AP® Courses, Chapter 24, Problem 34 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
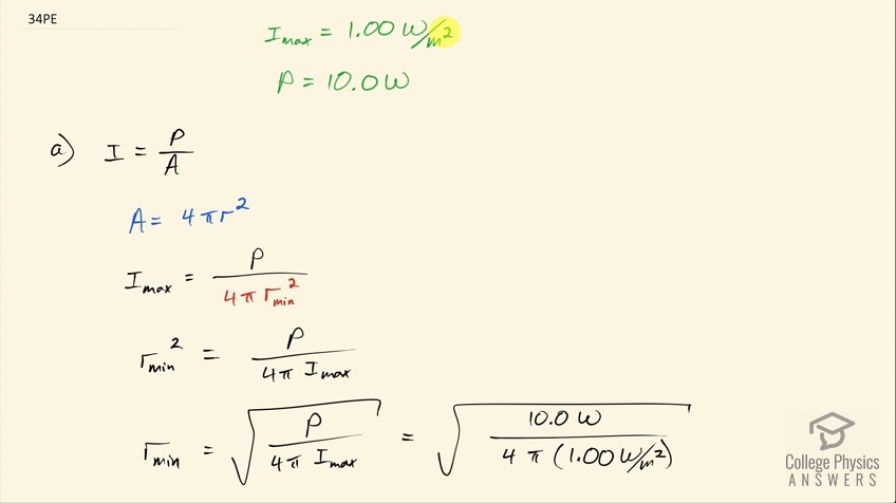
This is College Physics Answers with Shaun Dychko. The maximum safe intensity for microwave radiation hitting a person is 1.00 watt per square meter and suppose somebody is standing near a radar that's leaking some microwaves with a power of 10 watts of leakage and what distance should the person stand away from the machine in order to be safe? And so the machine might be here and it's emitting microwaves in all directions and that radiation is going to be distributed evenly a spherical area and that sphere increases in size the further away you go and so when you calculate the intensity— it's power divided by area— and so the bigger the area over which the microwave radiation is spread, the less the intensity so as area increases, this quotient decreases. And this area is the surface area of a sphere which has the formula 4π times radius squared so this radius is what we are going to be calculating for. We are gonna say that the maximum intensity is the power divided by this area 4π times minimum radius squared—this is the closest one can get while still being safe. So we are gonna solve for r min... first we'll solve for r min squared by multiplying both side by r min squared over maximum intensity and we get that the r min squared equals power divided by 4π times maximum intensity and then take the square root of both sides. And so the minimum distance away from the machine or the closest one can get while being safe in other words is the square root of the power divided by 4π times the maximum intensity. So that's square root of 10.0 watts divided by 4π times 1.00 watt per square meter and that is 0.892 meters. Part (b) is asking for the maximum electric field strength at the safe intensity. So intensity is speed of light times permittivity of free space times maximum electric field strength squared over 2 and we can solve for E naught by first multiplying both sides by 2 over cε naught and then we have E naught squared equals 2I over cε naught and then take the square root of both sides to solve for the peak electric field strength. So that's square root of 2 times the safe intensity which is 1.00 watt per square meter divided by speed of light times permittivity of free space and this is 27.4 newtons per coulomb.
