Question
An circuit containing a 1.00-pF capacitor oscillates at such a frequency that it radiates at a 300-nm wavelength. (a) What is the inductance of the circuit? (b) What is unreasonable about this result? (c) Which assumptions are unreasonable or inconsistent?
Final Answer
- The inductance is immeasurably small
- The wavelength is too small.
Solution video
OpenStax College Physics for AP® Courses, Chapter 24, Problem 50 (Problems & Exercises)
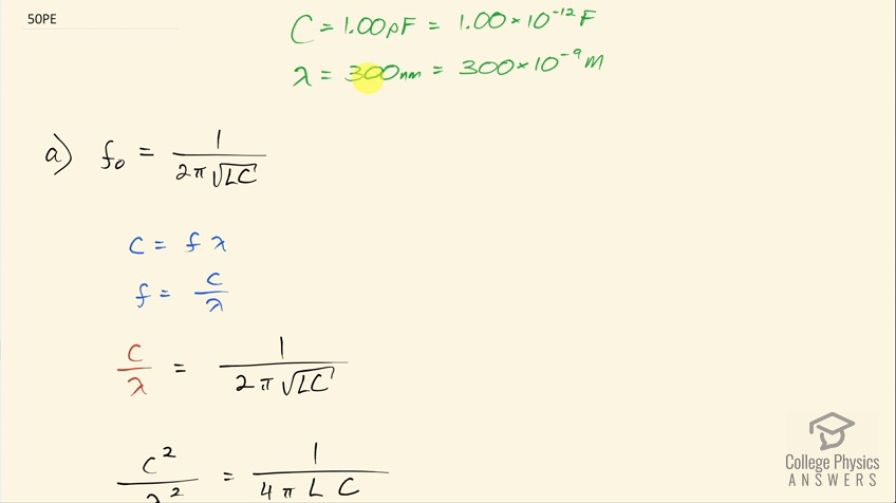
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A circuit consisting of an inductor and a capacitor oscillates such that it emits electromagnetic radiation with a wavelength of 300 nanometers, which is 300 times 10 to the minus 9 meters. It has a capacitor in it of 1.00 picofarad, which is 1.00 times 10 to the minus 12 farads and our question in part (a) is what is the inductance of the circuit? So LC-circuits resonate at a frequency of 1 over 2π times square root of inductance times capacitance and so we take this resonant frequency to be the frequency at which this light is being emitted and we can substitute for it in terms of wavelength that we know based on the wave formula. So the speed of light equals frequency times wavelength and we can solve for f by dividing both sides by λ and so f is c over λ in other words and then substitute that in place of the peak frequency in this formula so we have c over λ equals 1 over 2π times square root LC. We'll square both sides and then we have speed of light squared over λ squared equals 1 over 4π times... or π squared I should say times the inductance times the capacitance and this C here stands for capacitance whereas this one is the speed of light (it's a bit confusing but now that I mentioned it maybe it's OK) and we'll solve for the inductance by multiplying both sides by inductance times wavelength squared over speed of light squared. So the inductance then is λ squared over 4π squaredc squared times capacitance. So that's 300 times 10 to the minus 9 meters—wavelength—squared divided by 4π squared times speed of light squared times 1.00 times 10 to the minus 12 farads—capacitance— and that is 2.54 times 10 to the minus 20 henries; this inductance is too small to even be measurable and well, the wavelength must be too small in this information given to us. A picofarad capacitor is possible so this wavelength must be many orders of magnitude too small.
