Question
Naturally occurring is listed as responsible for 16
mrem/y of background radiation. Calculate the mass of that must be inside the 55-kg body of a woman to produce this dose. Each decay emits a 1.32-MeV , and 50% of the energy is absorbed inside the body.
Final Answer
Solution video
OpenStax College Physics, Chapter 32, Problem 22 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
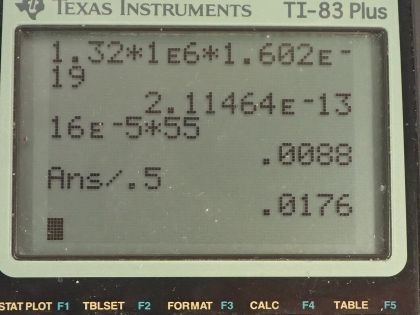
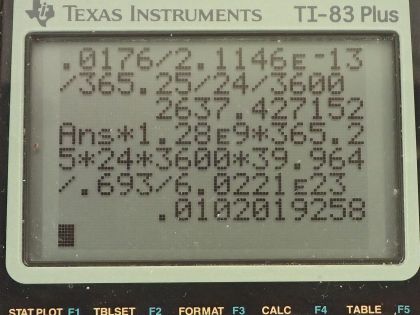
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. We are told that potassium-40 is responsible for 16 millirems per year of dose equivalent for a person and we are going to convert this into sieverts per year by multiplying by 1 sievert for every 100 rem and also converting the millirem into 16 times 10 to the minus 3 rems per year this is 16 times 10 to the minus 5 sieverts per year. The mass of a woman receiving this dose is 55 kilograms and we are asked to figure out what mass of potassium-40 must be in her body to produce this kind of dose equivalent? The molar mass of potassium-40 is 39.964 grams per mol we are told that each decay of potassium-40 emits a beta particle with an energy of 1.32 megaelectron volts so we'll convert that into joules by multiplying by 1 times 10 to the 6 electron volts per megaelectron volt and then multiply by 1.602 times 10 to the minus 19 joules per electron volt for an energy of 2.1146 times 10 to the minus 13 joules per decay. Only 50 percent of the decays are absorbed or 50 percent of the decay energy is absorbed by the body so that's the efficiency of how much energy produced is actually absorbed. The relative biological effectiveness for beta rays with an energy more than 32 kiloelectron volts is 1 and we will need that to turn this dose equivalent into dose absorbed and the last piece of data we need is the half-life of potassium-40, which is 1.28 times 10 to the 9 years so this is all the book keeping that we had to do to begin the question and it's good to take care of it here so that you don't have to think about it later when you are doing algebra and trying to work out the concepts. So let's first figure out what the absorbed dose is based on knowing the dose equivalent so we divide the dose equivalent by the relative biological effectiveness and numerically this makes no change but it turns it into 16 times 10 to the minus 5 joules per kilogram per year— the units are grays per year but I like to put joules per kilogram instead of grays; it's easier to see how the units cancel with units of joules per kilogram instead of grays per year. Okay! So what is the total energy absorbed? Well it's going to be the absorbed dose per year multiplied by the body mass so that's 16 times 10 to the minus 5 joules per kilogram per year times 55 kilograms and that's 0.0088 joules per year. Now knowing how much energy is absorbed by the body, let's figure out how much energy is produced knowing that the efficiency is the energy absorbed divided by the total produced and we can rearrange this to solve for energy produced and it's the energy absorbed divided by the efficiency. So that's 0.0088 joules per year divided by 0.50 and that is 0.0176 joules per year. Now we can figure out what the activity is of this potassium-40 in her body and it's the number of decays per time and this will be 0.0176 joules of total energy produced per year multiplied by 1 decay for every 2.1146 times 10 to the minus 13 joules and that's the reciprocal of this number here so we see that the joules cancel now and we have the number of decays per year and let's turn that into decays per second and we will have units of becquerels in that case. So we multiply by 1 year for every 365.25 days and then by 1 day for every 24 hours and then 1 hour for every 3600 seconds and we are left with decays per second and that is 2637.43 decays per second. Another formula for activity is 0.693 multiplied by the number of atoms divided by the half-life and here finally we can see how this relates to mass of potassium-40 because the number of atoms is the mass of potassium-40 divided by the molar mass of potassium-40 multiplied by Avogadro's number. So we'll substitute this in place of N and we have the activity then is 0.693 times the mass of potassium-40 times Avogadro's number divided by half-life times the molar mass of potassium-40. We'll rearrange this to solve for m by multiplying both sides by half-life and by the molar mass and divide both sides by 0.693 and divide by Avogadro's number so we do that here and we do it here too. So the mass then is 2637.43 becquerels multiplied by the half-life converted into seconds we could have saved ourselves a little bit of calculation by having left this in decays per year and it would not be becquerels anymore, it would be decays per year and then we can multiply that by this half-life in years and years would have canceled but anyway, this is the way it worked out so it's a good habit generally to use mks units. So we convert the years into seconds and then we multiply by the molar mass and divide by 0.693 and divide by Avogadro's number and we get 1.02 times 10 to the minus 2 grams of potassium-40 in this person's body.