A slightly deranged Arctic inventor surrounded by ice thinks it would be much less mechanically complex to cool a car engine by melting ice on it than by having a water-cooled system with a radiator, water pump, antifreeze, and so on. a) If 80.0% of the energy in 1.00 gal of gasoline is converted into “waste heat” in a car engine, how many kilograms of 0° C ice could it melt? b) Is this a reasonable amount of ice to carry around to cool the engine for 1.00 gal of gasoline consumption? c) What premises or assumptions are unreasonable?

a) 21 kg b) Yes, it's possible to carry this much ice, but many journeys are long enough to consume much more than 1 gallon of gasoline. Average fuel efficiency in the United States of America is 25 mpg, and it's common to travel further than 25 miles. For long journeys carrying ice will become impractical. c) Not all heat energy released by combustion goes into the engine. Much of it escapes through the exhaust. The practicality of obtaining so much ice is another problem with this cooling approach.

OpenStax College Physics for AP® Courses, Chapter 14, Problem 77 (Problems & Exercises)

In order to watch this solution you need to have a subscription.

Start free trial Log in

vote with a rating of votes with an average rating of .

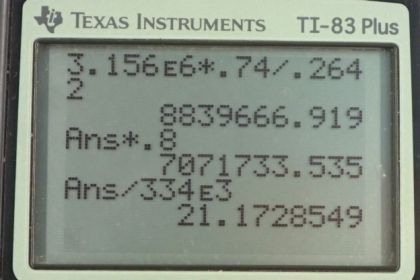
This is College Physics Answers with Shaun Dychko. In this question, we're going to see how practical it is to cool an engine using blocks of ice instead of the usual antifreeze liquid being circulated through the radiator and so on. So, to answer this question, we need to know what energy is released by burning gasoline. And, from Wikipedia, I found 3.156 times 10 to the 6 Joules is released per kilogram burned. And so, we're told that we're burning a gallon of gasoline. And so, we need to use this information, which is Joules per kilogram, and the gallon information to figure out Joules. So, we'll convert the kilograms into liters and using this conversion of liters per gallon and figure out how much energy is released. So, that's 3.156 times 10 to the 6 Joules per kilogram and times by 0.74 kilograms per liter, that's the density of gasoline that I also looked up on Wikipedia. And then, multiply by one liter for every 0.2642 gallons. So the gallons cancel, the liters cancel, the kilograms cancel and we're left with Joules. 8.8397 times 10 to the 6 Joules. Now, 80% of this is going to be absorbed by the engine supposedly. So, we have 0.80 times that answer, giving us 7.0717 times 10 to the 6 Joules of thermal energy to dissipate using the ice. And, this formula here tells us the amount of heat of fusion would be absorbed by the ice melting and we'll solve for this mass by dividing both sides by the latent heat of fusion. And so, the mass of ice that will be needed to cool this engine is going to be the amount of thermal energy it has to dissipate divided by the latent heat of fusion, so that's 7.0717 times 10 to the 6 Joules divided by 334 times 10 to the 3 Joules per kilogram which is 21 kilograms. Now, it is possible to carry around this much ice, but many journeys are longer and will consume more than just one gallon of gasoline. So average fuel efficiency in the USA, I looked up, is 25 miles per gallon. And, it's common to travel further than 25 miles, so it's common to use more than one gallon. So, for long journeys, carrying ice will become impractical because this is 43 or 44 pounds or so, so that's quite heavy and unrealistic to carry much more than that. So, some of the assumptions that are dubious is that not all heat energy released by combustion goes into the engine. A lot of it escapes through the exhaust. The practicality of obtaining so much ice is unreasonable.