Question
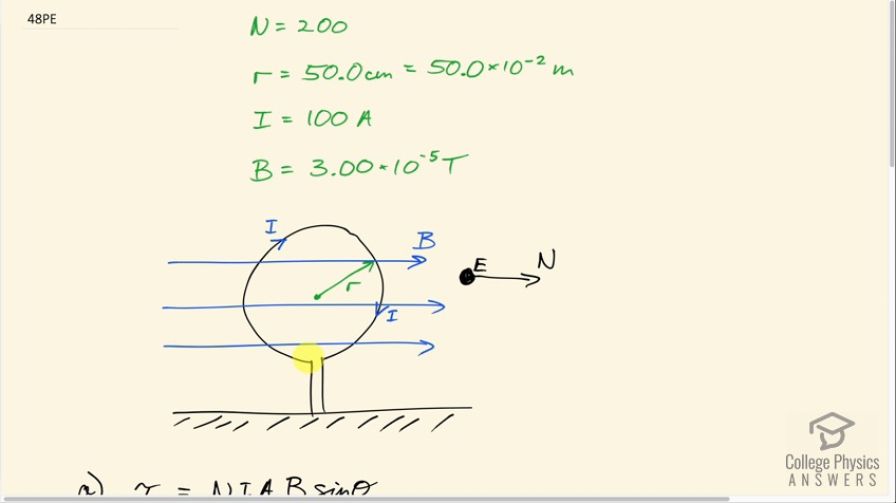
(a) A 200-turn circular loop of radius 50.0 cm is vertical, with its axis on an east-west line. A current of 100 A circulates clockwise in the loop when viewed from the east. The Earth’s field here is due north, parallel to the ground, with a strength of . What are the direction and magnitude of the torque on the loop? (b) Does this device have any practical applications as a motor?
Final Answer
- , clockwise when viewed from above.
- Whether this motor has practical applications depends on how the loop is connected to the source of the current. The curent needs to always be clockwise when viewed from the East, which requires the contacts to switch polarity every half rotation. The question doesn't tell us if this is the case. Without this kind of connection, the loop will oscillate back and forth, which limits its practical applications.
Solution video
OpenStax College Physics, Chapter 22, Problem 48 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. In this question we really have to draw a picture in order to understand all the directions that are given to us by the question. So we have a loop of wire that's vertical so that means we can draw the ground here and put the loop standing up like this and we are going to look at it from the East because we are told that the direction of current is clockwise when this loop is viewed from the East and that means we have North to the right hand side here and East is coming towards us because we are in the easterly position so we are looking at this from the East and so East is coming towards us and we are looking towards the West— West would be an x away from us— and the magnetic field of the Earth is parallel to the ground, pointing to the North and we have a radius of the loop that we are given—50.0 centimeters— the number of turns is 200, it's carrying 100 amps of current and the magnetic field strength of the Earth is 3.00 times 10 to the minus 5 tesla here and the question is what is the direction and magnitude of the torque on the loop? Well, we can figure out the direction using our right-hand rule so we will point our many fingers in the direction of these many magnetic field lines and I used the word 'many' there to help you remember that many fingers point along magnetic fields lines because there are many of those lines and then our thumb points in the direction of current, let's consider this position here. The current is upwards on this left hand side... I hesitate to use the word left hand though because it's the right hand rule that we are using here but anyway... we are in this area of the loop here, our fingers are pointing to the right, our thumb is pointing up and our palm is pushing on the direction of force on those current carrying segment of wire here and that is into the page so the force at this position is into the page. And then if you do the same analysis on the other side, you have your thumb pointing down while your fingers are pointing to the right and your palm is facing towards you or out of the page and so this is causing a torque because it's in on the one side of the axis of rotation and it's out of the page on the other side of the axis of rotation. So if you were to look at this loop from above, you would see it moving clockwise. So if you had some eyeballs that were here then you would see a clockwise rotation from above. Okay! And then the next question is what is the magnitude of that torque? Well, the torque is the number of turns times the current in the loop times the area of the loop multiplied by the magnetic field strength times sin of the angle between the perpendicular to the plane of the loop and the magnetic field, which in this case is 90. Now the area being a circle here is π times its radius squared and so we substitute that in place of area and so the torque then is NIπr squaredB times sin Θ. So N is 200 turns, I is 100 amps π times the radius written in meters 50.0 times 10 to the minus 2 meters squared times 3.00 times 10 to the minus 5 tesla times sin 90 degrees and that is 0.471 newton meters and that's clockwise when viewed from above. Part (b) asks does this device have any practical applications as a motor? Well, it depends on how the loop is connected to the source of the current. The current needs to always be clockwise when viewed from the East which requires the contacts to switch polarity every half rotation. So this contact might be connected to the positive as the way I have drawn the current right now. So this is the positive contact and this is the negative contact but when it rotates, the side that ends up in the left hand position here needs to still be positive in order to have the current still be moving clockwise when viewed from the East and so that means that this wire here, which will now be on the left hand side after one half rotation, needs to be connected to the positive terminal of the current source and so the little gizmo that does this in a regular motor are called brushes and they are like... made out of carbon and they are like loops that are broken in half and they switch the polarity of these contacts here as this thing goes around. So I don't know... the question doesn't tell us much about this so we can't really say for sure whether it would be good as a motor but as it is if this remains positive and this piece of wire here remains negative when they switch around, the current will be going in the other direction and then the torque will be in the opposite sense and then this thing will oscillate back and forth, which could have its applications too but it will have limits on its applications that are possible. There!
