Question
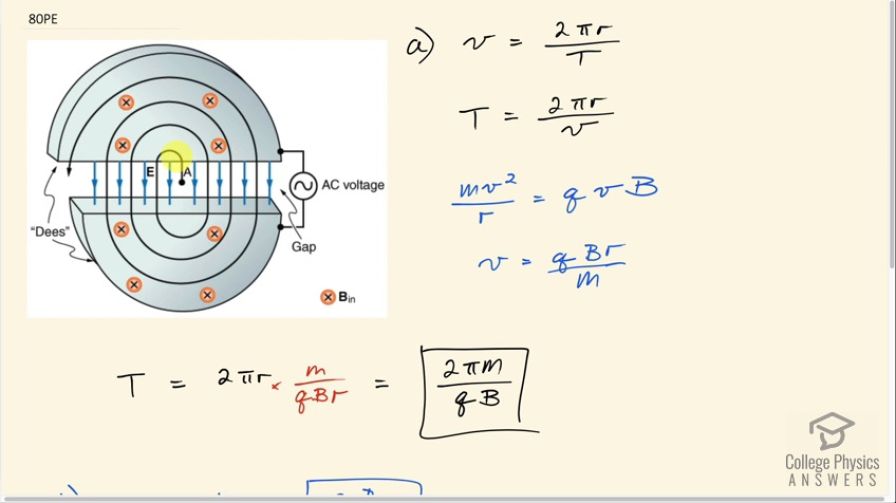
(a) Show that the period of the circular orbit of a charged particle moving perpendicularly to a uniform magnetic field is T=2πmqBT = \dfrac{2 \pi m}{qB}. (b) What is the frequency ff? (c) What is the angular velocity ω\omega ? Note that these results are independent of the velocity and radius of the orbit and, hence, of the energy of the particle. (Figure 22.64.)
<b>Figure 22.64</b> Cyclotrons accelerate charged particles orbiting in a magnetic field by placing an AC voltage on the metal Dees, between which the particles move, so that energy is added twice each orbit. The frequency is constant, since it is independent of the particle energy—the radius of the orbit simply increases with energy until the particles approach the edge and are extracted for various experiments and applications.
Figure 22.64 Cyclotrons accelerate charged particles orbiting in a magnetic field by placing an AC voltage on the metal Dees, between which the particles move, so that energy is added twice each orbit. The frequency is constant, since it is independent of the particle energy—the radius of the orbit simply increases with energy until the particles approach the edge and are extracted for various experiments and applications.
Question by OpenStax is licensed under CC BY 4.0
Final Answer
  1. Please see the solution video.
  2. qB2πm\dfrac{qB}{2 \pi m}
  3. qBm\dfrac{qB}{m}

Solution video

OpenStax College Physics, Chapter 22, Problem 80 (Problems & Exercises)

OpenStax College Physics, Chapter 22, Problem 80 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right
Video Transcript
This is College Physics Answers with Shaun Dychko. In a cyclotron, a charged particle starts in the center with a little bit of velocity and then this magnetic field will cause it to go into a curve and then it gets accelerated across this gap between the Dees by this electric field so if it's a positively charged particle, it will get accelerated down here and then it will encounter this region where there is magnetic field causing it to move in a circular path again and then once it crosses this gap, it gets accelerated again but once it reaches here, the direction of this magnetic field or sorry the electric field in blue here will change because this is an alternating current voltage and so it gets accelerated upwards once it gets to this point and then it goes in a circle again and then the AC switches at the exact moment when the charged particle reaches this edge of the Dee and then the field will be pointing down, it gets accelerated faster still and its radius is increasing due to its increasing energy but its period and its frequency are remaining the same as we are going to derive here. So we are going to show that the period of one complete circle for a charged particle is 2π times the particle's mass divided by its charge times the magnetic field strength. So speed of the particle is the distance it travels divided by time so period is the time it takes to travel one complete circle and so we have the circumference of a circle here— 2π times radius—divided by period and we can solve this for period then by multiplying both sides by period divided by speed. So period then is 2πr over v. And we can use this Lorentz Force formula for figuring out what v is. So the Lorentz force is providing the centripetal force, which is mv squared over r for any particle moving in a circle with no tangental acceleration. So we have mass of the particle times its speed squared divided by r is the charge times its speed times magnetic field strength and we can solve this for v by multiplying both sides by r over m and then also divide both sides by v. So we have v to the power of 1 on the left equals qBr over m and that we can substitute in for v here and so we are having 2πr divided by this fraction but dividing by a fraction I find more easy to express as multiplying by its reciprocal because I don't like to have fractions within fractions. So we have 2πr multiplied by the flipped version of this it's the reciprocal in other words, m over qBr, the r's cancel leaving us with 2π times mass divided by charge times magnetic field strength and this is what we wanted to show that the period of making one complete circle for a charge particle in this cyclotron is 2π times its mass divided by its charge times magnetic field. Frequency is the reciprocal of period so we just flip this fraction qB over 2πm and then in part (c), we are asked to find the angular velocity and so it does one complete circle, which has 2π radians in an amount of time equal to the period because that's what period is in this case, the time it takes to do one complete cycle, which is a circle. And so we have 2π divided by period and that is 2π times the reciprocal of this so 2π times qB over 2πm and this works out to qB over m. So the angular velocity depends only on the charge, the magnetic field strength and the mass.