Question
A 75.0-kg person climbs stairs, gaining 2.50 meters in height. Find the work done to accomplish this task.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

1.84×103 J1.84\times 10^{3}\textrm{ J}

Solution video

OpenStax College Physics, Chapter 7, Problem 2 (Problems & Exercises)

OpenStax College Physics, Chapter 7, Problem 2 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 7, Problem 2 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. Question asks how much work is done when this person climbs the stairs of height 2.5 meters and they have a mass of 75.0 kilograms. Well there are a few assumptions that the question is making: first they are assuming that it's the work done by the person that we are interested in because the total work done, if you consider the person and gravity, is zero because the amount of work that the person does— which is positive—is equal to the amount of work that the gravity is doing—which is negative. Okay! Anyway so we assume that its the work done by the person that we are interested in and we also assume that the person is going at constant speed that's important because that means this force upwards that they are applying to get themselves up the stairs is equal in magnitude to the gravity. So two assumptions that are not explicitly written in the question but you have to be aware of them. Okay! So the work done by the person climbing the stairs at constant speed. So work is the force applied and the component of which is parallel to the displacement and in this case, the displacement is straight up and this force that they are applying is straight up. We assume that there's no force going sideways anymore; there would have been a sideways force to begin with, you know, on the ground here to get them up to speed horizontally but now once they have some horizontal speed, we assume that there is no need for any more force horizontally. Okay! So the only force then is straight up and then that force is gonna be equal to gravity downwards and the displacement is equal to this height h that they are going up and we plug in numbers. So 75.0 kilograms times 9.8 newtons per kilogram times 2.50 meters and this makes 1.84 times 10 to the 3 joules of work done.

Comments

Hi Shaun,

How do we find the angle for this equation. Since in the book W= F*D* (Cos angle)?

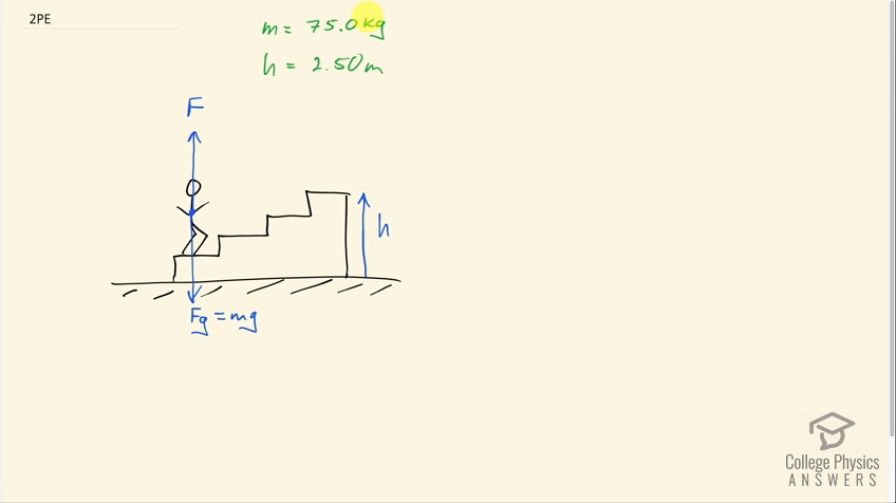
Hello phillip and samuel, thanks for the question. There is a simplifying assumption here that the direction of force applied is straight up. Granted, the person would have exerted a horizontal force in the beginning to initiate the horizontal component of their motion, but that was for a brief moment before we begin our analysis. There is no horizontal friction, and there is no horizontal acceleration, so the person doesn't need to exert a horizontal force after that initial, ignored, moment. OK - the person exerts a force straight up. Next we need to think about the direction of their displacement, which is the DD in W=FDcos⁡θW = FD\cos{\theta}. Strictly speaking, it's on an angle above horizontal to the right - it's along the stairs in other words. Suppose we knew that angle, and let's call it α\alpha since it isn't quite the correct angle to use in the work formula, what would we do with it? Keep in mind this is the angle between displacement and horizontal. We would find the angle between the force and the displacement (since that's the angle θ\theta in the formula), and θ=90∘−α\theta = 90^\circ - \alpha. Having now found θ\theta we could multiply it by the displacement, as suggested by W=FDcos⁡θW = FD\cos{\theta}, and then get our answer, and if I'm understanding correctly, your question is - none of this is possible in this question since I don't know the angle, right? Well, the angle isn't necessary. Consider, hypothetically, that you do finally have θ\theta and you multiply the cosine of it by the displacement, what does that give you? It gives the vertical component of the displacement. We already know the vertical component of the displacement - it's the height of the stairs! That's something we already know, so we can carry on without needing the angle. Work is the force multiplied by the component of displacement that's in the same direction as the force - that's the meaning of W=FDcos⁡θW = FD\cos{\theta}.
Hope this helps,
Shaun