Question
The awe-inspiring Great Pyramid of Cheops was built more than 4500 years ago. Its square base, originally 230 m on a side, covered 13.1 acres, and it was 146 m high, with a mass of about . (The pyramid’s dimensions are slightly different today due to quarrying and some sagging.) Historians estimate that 20,000 workers spent 20 years to construct it, working 12-hour days, 330 days per year. (a) Calculate the gravitational potential energy stored in the pyramid, given its center of mass is at one-fourth its height. (b) Only a fraction of the workers lifted blocks; most were involved in support services such as building ramps (see Figure 7.44), bringing food and water, and hauling blocks to the site. Calculate the efficiency of the workers who did the lifting, assuming there were 1000 of them and they consumed food energy at the rate of 300 kcal/h. What does your answer imply about how much of their work went into block-lifting, versus how much work went into friction and lifting and lowering their own bodies? (c) Calculate the mass of food that had to be supplied each day, assuming that the average worker required 3600 kcal per day and that their diet was 5% protein, 60% carbohydrate, and 35% fat. (These proportions neglect the mass of bulk and nondigestible materials consumed.)
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 58 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
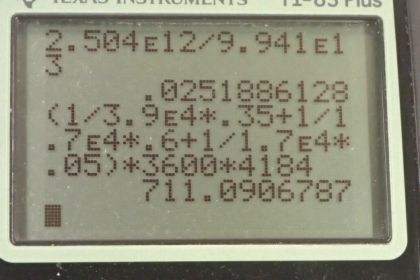
This is College Physics Answers with Shaun Dychko. The Great Pyramid of Cheops built 4500 years ago has a gravitational potential energy of the total mass of all the stones which is 7 times 10 to the 9 kilograms multiplied by gravitational field strength— which is 9.8 newtons per kilogram— multiplied by the height of the center of mass which is the height of the peak divided by 4 we are told— we are told that the center of mass is one-quarter way up to the peak; this works out to 2.5 times 10 to the 12 joules. Now the efficiency of the 1000 workers that are actually lifting blocks is going to be the total work that they accomplish the work output which is this gravitational potential energy given to the blocks in other words that work output is divided by the total energy consumed by the workers in doing that work. So the energy consumed then is going to be this 1000 workers that are doing the lifting multiplied by the 300 kilocalories that they consume per hour multiplied by the amount of time that they spent working and then convert these kilocalories into joules. So we are multiplying by 12 hours worked per day times 330 days worked per year times the 20 years it took to build this thing multiplied by 4184 joules for every kilocalorie so the kilocalories cancel and we are left with 9.9 times 10 to the 13 joules is the total energy consumed by all the workers. So the efficiency then is this gravitational potential energy that the blocks have— 2.504 times 10 to the 12 joules— divided by this energy consumed and that is an efficiency of 2.5%. Now part (c) we are gonna calculate how much mass of food is needed for all the workers working on this pyramid. So there are a total of 20,000 workers and we are gonna calculate the mass of food to feed one worker. And first we find a weighted average of all the different food types— fats, carbohydrates, and proteins— and the average is... this is weighted by the proportion that each type makes of the total so 35% percent is fat and 60% is carbohydrates and 5% is protein and then that gives us grams per joule and then we multiply by the number of joules consumed per worker during this conversion between kilocalories and joules as well. So there's 1 gram of fat in every 3.9 times 10 to the 4 joules according to this table [7.1] and we find that entry here and that's multiplied by 0.35 and then 1 gram of carbohydrate gives 1.7 times 10 to the 4 joules that's multiplied by 0.60 and then add to that 1 gram of protein for the same amount of joules multiply by 0.05. You could find the number of grams just for fat by taking this and then multiplying it by 3600 but since each of these terms is going to get multiplied by 3600, I'm factoring that out and writing this bracket around all three terms. So we multiply by 3600 kilocalories per worker and that gives us the number of kilocalories needed and then we convert that into joules so that's 711.09 grams per worker. And then we multiply that by 20,000 workers and then convert it into kilograms and we see that it takes 14000 kilograms of food to keep these workers going everyday and that's why many of them were involved just in providing food.