OpenStax College Physics, Chapter 7, Problem 43 (Problems & Exercises)

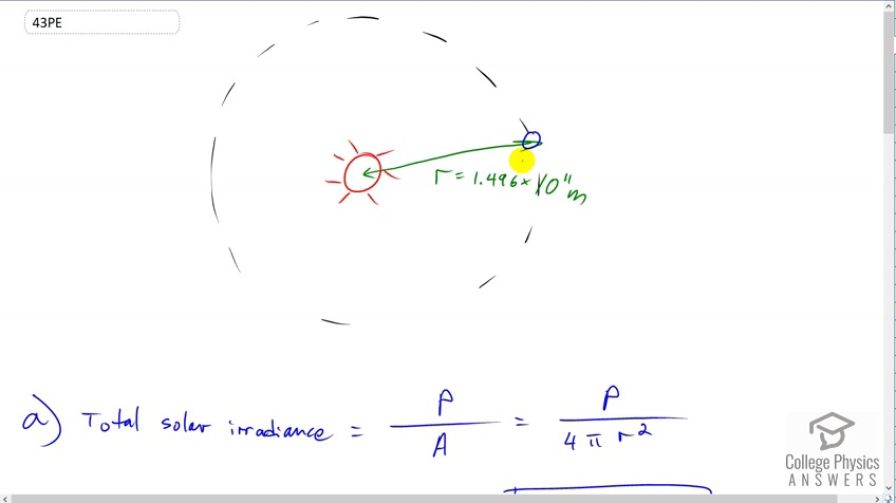
This is College Physics Answers with Shaun Dychko. This question asks us to find out what is the power per square meter due to the sun at the position of the earth. There is a special name for this number, it's called the total solar irradiance. We can calculate it by noticing that the total power output of the sun is going to be distributed over a sphere at this radius here. I can only draw a circle of course but you can imagine a three dimensional sphere here and the power is distributed over that entire sphere. So to find the solar irradiance we take the power and divide it by the area of that sphere. The area of a sphere is four pi r squared. So r is going to be the distance from the sun to the earth. So we have four times ten to the twenty-six watts of total power output of the sun divided by four times pi times 1.496 times ten to the eleven meters squared, giving us 1.42 kilowatts per square meter. Now, in part B we're told that the solar irradiance due to a bit being reflected by the atmosphere particularly by the clouds and some being absorbed in the atmosphere, that the amount of power per square meter that reaches the earth's surface is only 1.3. Now, given that a typical power plant might make 750 megawatts which I've written as times ten to the six watts, what area of solar panels would be needed given an efficiency of two percent? That's the efficiency by which the solar panels convert this power per square meter received from the sun into electricity. We're asked to find the area in square kilometers and so this is going to be in units of meters because we have meters there and we multiply by one kilometer for every 1000 meters and we do it twice because we're using square meters and so we have to square this conversion factor as well. So we've 750 times ten to the six watts divided by 1.3 times ten to the three watts per square meter solar irradiance, times the two percent efficiency and this gives us 28.8 square kilometers. Now, maybe I should explain where this formula came from a bit. The power output of the electrical panels equals the solar irradiance which has units of power per square meter multiplied by the area of the solar panels which has meters squared. So this gives us the meters squared in the denominator of the solar irradiance we get multiplied by the square meters of the area of the electrical panels and then we have a certain efficiency factor here of two percent. We multiply by the efficiency as well and that gives us the power output of the panels. Then we rearrange that to solve for the area of the panels by dividing both sides by solar irradiance and dividing by efficiency. Okay. So 28.8 square kilometers, not bad for replacing a power plant. Now we're asked to figure what area of solar panels would be needed to meet the entire current energy demands of the United States, Australia and China in a year. Since we're going to be doing a bunch of calculations using kind of the same numbers, to reduce the amount of writing we have to do I'm going to figure out some factors here to plug in for shortcuts. So we're going to be substituting a different number for power. We're going to be re-using this formula, substituting a different number in for power for each country. We're going to be dividing by the same solar irradiance and the same efficiency and have the same conversion factor so let's take all of that stuff that's going to be the same between the three different calculations for the three different countries and turn it into a single number that we can multiply by. So we have one divided by the 1.3 times ten to the three watts per square meter for solar irradiance and then multiply by two percent on the bottom there and then multiply by this conversion factor giving us 3.84615 times ten to the minus eight square kilometers per watt. So you know this is a number which I couldn't think of a better letter than just z. This is a number that represents the number of square kilometers the solar panel that are needed to generate each watt of power output. So of course a watt is a small amount of power, one watt, and a square kilometer is a very big area and so we expect to get a really small number for the number of square kilometers per watt needed. Then, we're going to be converting energy that is given to us in the question into power by dividing by the number of seconds in a year. At least we assume that -- I mean it says these energy consumption values are from 2006 so that suggests that these energy consumption values are each for the duration of one year. So, we need to find the number of seconds in a year to convert those energies into powers. So we have the time in a year in seconds is one year times 365 and a quarter days per year times 24 hours per day times 3600 seconds per hour, giving us 3.1558 times ten to the seven seconds per year. So, considering the US, the amount of area of solar panels needed to generate the US's total energy demands for one year is 1.05 times ten to the twenty joules consumed per year, multiplied by one year for every 3.1558 times ten to the seven seconds. This gives us joules per second which is a longer way of writing watts. So the units are now watts, watts are joules per second. Then we multiply by 3.84615 times ten to the minus six -- sorry about that -- ten to the minus eight, you can see it, kilometers squared per watt and the watts in the denominator there cancel with these watts that are actually here giving us square kilometers. So this is 128 thousand square kilometers of solar panels would be needed which is a pretty big number. Then for Australia the only thing that changes is that we're substituting 5.4 times ten to the eighteen joules per year, the other numbers are the same. This gives us six thousand six hundred square kilometers of solar panels needed for Australia for a year. Then for China we have 6.3 times ten to the nineteen joules per year and this works out to 77 thousand square kilometers of solar panels needed to meet its energy demands.