Question
A hydroelectric power facility (see Figure 7.37) converts the gravitational potential energy of water behind a dam to electric energy. (a) What is the gravitational potential energy relative to the generators of a lake of volume ( mass = ), given that the lake has an average height of 40.0 m above the generators? (b) Compare this with the energy stored in a 9-megaton fusion bomb.
Final Answer
Solution video
OpenStax College Physics, Chapter 7, Problem 16 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
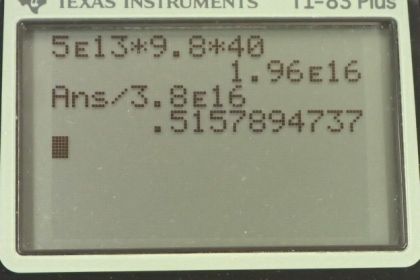
This is College Physics Answers with Shaun Dychko. This hydroelectric facility is holding back water with a massive 5 times 10 to the 13 kilograms, and the average height of the water is 40.0 meters. The question in part A is, what is the potential energy of all this water that could conceivably be turned into electrical energy. Although of course, the generators will have some inefficiency and the conversion won't be perfect, but this is the amount of energy that we're starting with anyhow, in the water. The gravitational potential energy is the mass of the water times gravitational fields strength g times the average height of the water, and that is 5 times 10 to the 13 kilograms times 9.8 times 40 meters, which gives 1.96 times 10 to the 16 Joules. We're told to compare this to the energy in a 9-Megaton fusion bomb. Table 7.1 has that figure which is 3.8 times 10 to the 16 Joules released in a 9-Megaton fusion bomb and divided that into 1.96 times 10 to the 16 Joules, gravitational potential energy and all this water is about 0.52. The energy contained in the position of this water and its gravitational potential energy is 0.52 times that of the energy released in a 9-Megaton fusion bomb.