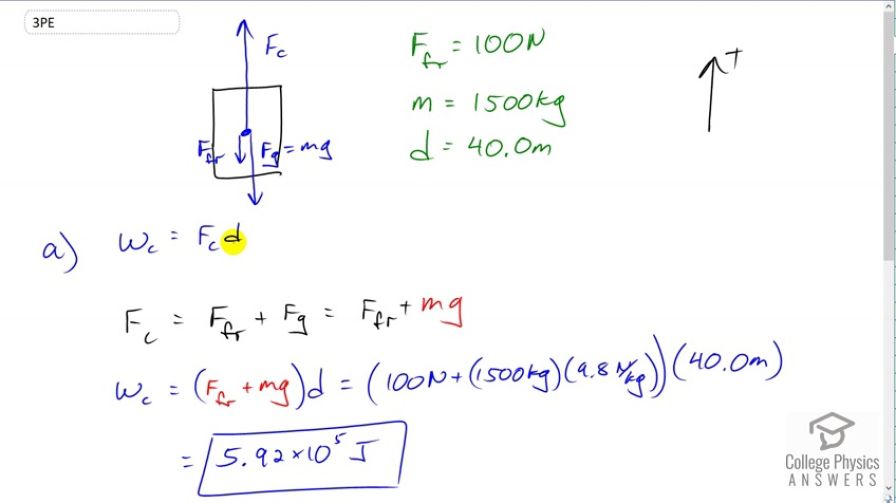
a)
b)
c)
Solution video
OpenStax College Physics, Chapter 7, Problem 3 (Problems & Exercises)
Calculator Screenshots
Comments
i used these exact methods to solve my problems and they came out wrong every time. Help please.
Hi brussell, I know physics can take a lot of effort to master. If you have more specific questions, please post them below the solutions, and we'll see what we can do.
For part b did we neglect the force of friction on purpose ?
Hi @angel.bryant, thank you for the question. Part (b) is asking for the work done by gravity, which is the force due to gravity times the displacement, and the answer will be the same whether there is friction or not. The friction causes the acceleration of the elevator to be different that it would be without friction, but the work done by gravity depends only on the force due to gravity (which is dependent only on the elevator mass, times ) and the height the elevator was lifted.
Hope this helps,
Shaun
Part (a) for g, why did you use instead of . Either way the units cancel and add up correctly( since one netwon is , but im just confused why you used that unit to begin with.
Hi fred444,
Thanks for the question. This is just a personal preference. To me, in the context of work and force, I think of as a gravitational field strength, for which seems more suitable. is often introduced in the context of kinematics where it's thought of as the acceleration due to gravity, in which case seems more suitable.
Hope that helps,
Shaun


