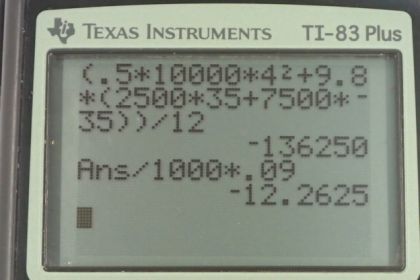
a)
b) 4.08 cents
Note: For part (b) the video calculates the cost per hour, rather than the cost to raise the elevator for 12 seconds. Multiplying the cost per hour by 12 seconds, and by 1 hr per 3600 seconds, gives the correct final answer of 4.08 cents. The calculator screenshot shows this final calculation.Solution video
OpenStax College Physics, Chapter 7, Problem 39 (Problems & Exercises)
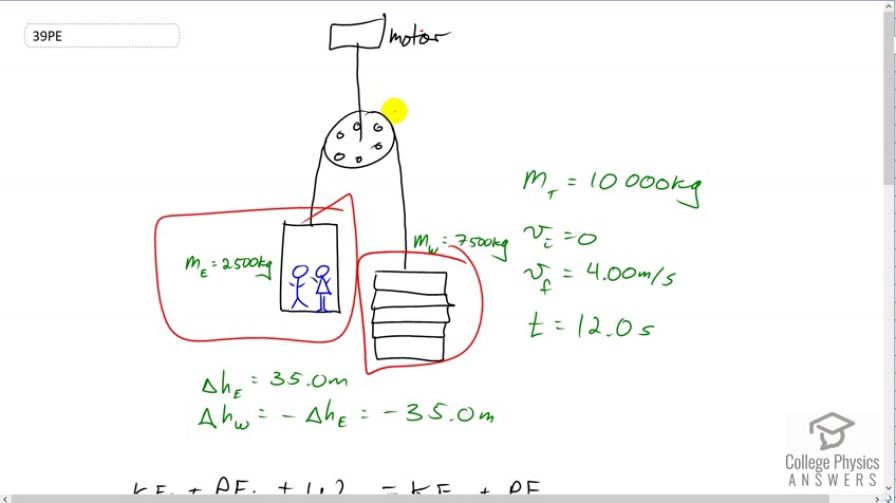
Calculator Screenshots
Comments
Part (b) asks for the cost to raise the elevator the height in part (a) - which means that you need to multiply the cost per unit time by the time (12 s) - the final answer is 4.087 cents.
Thank you very much for spotting this! I have updated the final answer and added a calculator screenshot to show the final calculation.
I understand the kinetic and potential energies of the elevator, but I'm a bit confused why the counterbalance potential is included. If the counter balance potential energy, wouldn't we have to include it's final kinetic energy too?
Perhaps it's because it's talking about the system as a whole. The kinetic energy of the entire system, which does include both elevator and counterweight. However, if the final Counterweight KE is 0, I could see why it was left out. Over all - That's how my mind has diagnosed it. I could be wrong. --Shaun?
Thank you for the question Russell. The kinetic energy of the counterweight is definitely included. At 1:41 I mention that the mass in the kinetic energy term is the total mass of the system, which is to say the mass of the counterweight plus the mass of the elevator with occupants. The potential energy has two terms - one for each mass - since the masses move differently. The counterweight moves negative 35.0 m, whereas the elevator moves positive 35.0 m. Considering kinetic energy, however, they each move with the same speed so their respective kinetic energy terms can be collected into one term. In other words: , where the final expression has with the subscript T for total mass which is what's shown in the video.
Hope this helps,
Shaun
Doesn't the question specify that the counterbalance does not gain height, only acceleration?
Why don't you substitute in acceleration due to gravity as negative if your upwards direction is positive?