Question
(a) Calculate the angle at which a wide slit
produces its first minimum for 410-nm violet light. (b) Where is the first minimum for 700-nm red light?
Final Answer
Solution video
OpenStax College Physics, Chapter 27, Problem 44 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
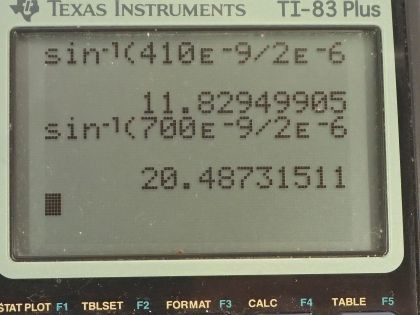
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. 410 nanometer light is incident on a single slit with a width of 2.00 micrometers and we want to find the very first minimum we want to find out what angle is it to that first minimum in the diffraction pattern? So the slit width then is 2.00 times 10 to the minus 6 meters and the wavelength we are working with is 410 times 10 to the minus 9 meters. So here's our formula for the minima when looking at a diffraction pattern through a single slit this is the size of the slit times sin of the angle to the minimum equals its order times the wavelength. So we'll solve for sin Θ first by dividing both sides by D so sin Θ is mλ over D and then we take the inverse sin of both sides and we get the angle then is inverse sin of the order times the wavelength divided by the slit width. So that's the inverse sin of 1 times 410 times 10 to the minus 9 meters divided by 2.00 times 10 to the minus 6 meters and that's 11.8 degrees. Now part (b) is asking where would the first minimum be for 700 nanometer light? And so the formula's the same but we have 700 here instead of 410 and the angle will be 20.5 degrees.
Comments
Why do you not use the destructive interference equation (m+1/2), for this problem if it is at a minimum?
Hi foothilldragon, thank you for your question. I think you mean the formula for destructive interference for a double slit? This question instead is looking for destructive interference in the diffraction pattern of a single slit, which is formula 27.21, instead of formula 27.4.
Hope this helps,
Shaun