Question
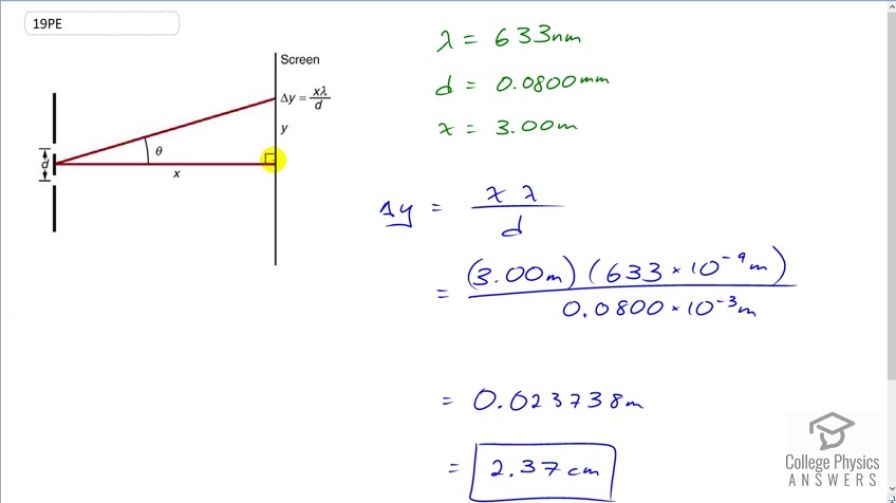
Using Δy=xλd\Delta y = \dfrac{x\lambda}{d}, calculate the distance between fringes for 633-nm light falling on double slits separated by 0.0800 mm, located 3.00 m from a screen as in Figure 27.56.
<b>Figure 27.56</b> The distance between adjacent fringes is a function of the distance to the screen, wavelength, and slit separation, assuming the slit separation is large compared with the wavelength.
Figure 27.56 The distance between adjacent fringes is a function of the distance to the screen, wavelength, and slit separation, assuming the slit separation is large compared with the wavelength.
Question by OpenStax is licensed under CC BY 4.0
Final Answer

2.37 cm2.37 \textrm{ cm}

Solution video

OpenStax College Physics, Chapter 27, Problem 19 (Problems & Exercises)

OpenStax College Physics, Chapter 27, Problem 19 (PE) video thumbnail

In order to watch this solution you need to have a subscription.

Start free trial Log in
vote with a rating of votes with an average rating of .
Chevron left Prev
Next Chevron right

Calculator Screenshots

  • OpenStax College Physics, Chapter 27, Problem 19 (PE) calculator screenshot 1
Video Transcript
This is College Physics Answers with Shaun Dychko. We're given an approximation for the separation on a screen between fringes in the interference pattern from the double slit experiment and it is the distance to the screen, which is X times the wavelength, divided by D, which is the separation between the slits. And, we're given all these information here where the distance to the screen is three meters and the separation between slits is 0.08 millimeters and the wavelength is 633 nanometers. So, the separation between the fringes then, Delta Y is going to be X Lambda over D, which is three meters times 633 times ten to the minus nine meters, divided by 0.08 times ten to the minus three meters, which is 0.0237838 meters, which, converted to centimeters, is 2.37 centimeters.