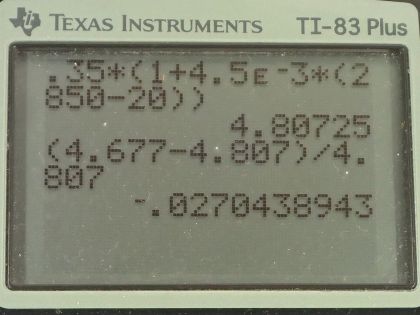
(a) Redo Example 20.6 taking into account the thermal expansion of the tungsten filament. You may assume a thermal expansion coefficient of . (b) By what percentage does your answer differ from that in the example?
Example 20.6: Although caution must be used in applying and for temperature changes greater than , for tungsten the equations work reasonably well for very large temperature changes. What, then, is the resistance of the tungsten filament in the previous example if its temperature is increased from room temperature ( ) to a typical operating temperature of ?
Example 20.5: A car headlight filament is made of tungsten and has a cold resistance of . If the filament is a cylinder 4.00 cm long (it may be coiled to save space), what is its diameter? Solution:
Solution video
OpenStax College Physics, Chapter 20, Problem 38 (Problems & Exercises)