OpenStax College Physics, Chapter 20, Problem 17 (Problems & Exercises)

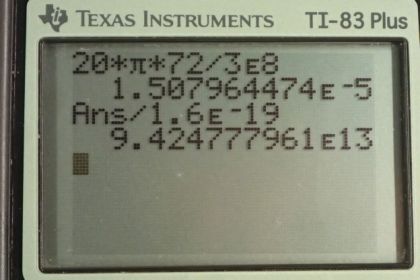
This is College Physics Answers with Shaun Dychko. We're going to figure out the number of electrons in the electron beam inside this storage ring at the Stanford Linear Accelerator. We know the current is the number of charges divided by time and we can solve this for Q by multiplying both sides by t and switching the sides around. The question is what should t be? We're given the current is 20 amps and we're given some other information about the size of this thing. But t should be the time it takes for the charge to make one complete lap around this toroid, that's the name of this donut shaped tube is a toroid because if we were to take a period of time longer than that, then we would be counting the same electron twice because it would be passing this position more than once. So we want the time it takes the beginning of the beam to return to the start. So that's going to be the distance it travels which is the circumference of this circle which is pi times its diameter, divided by the speed at which it goes which we're given is approximately the speed of light. So we'll substitute this in for t and so we have the charge then is the current times pi d over v. So that's 20 amps times pi, times 72 meters diameter, divided by thee times ten to the eight meters per second, speed of light. That gives this many coulombs and then we convert that into number of electrons by multiplying the coulombs by the number of electrons per coulomb. So this is one electron for every 1.6 times ten to the minus nineteen coulombs and dividing that into our answer for the number of coulombs gives us 9.42 times ten to the thirteen electrons.