Question
Show that the units , as implied by the equation .
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 20, Problem 46 (Problems & Exercises)
vote with a rating of
votes with an average rating of
.
Video Transcript
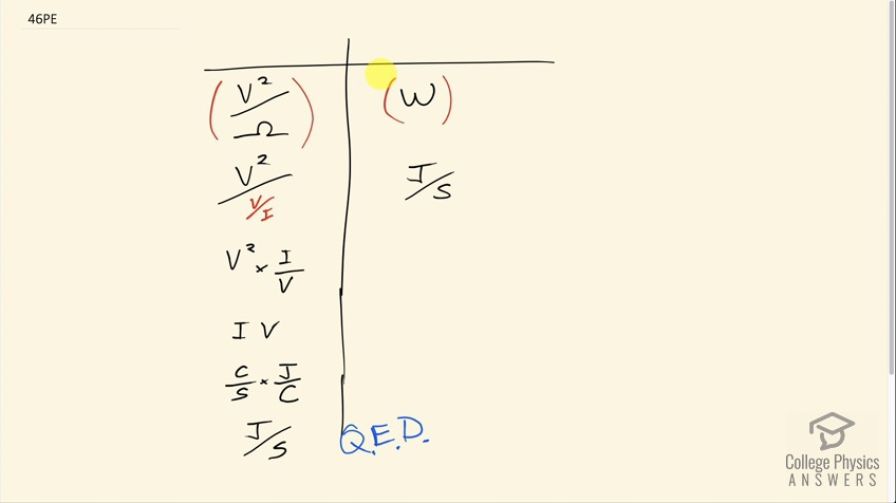
This is College Physics Answers with Shaun Dychko. We are going to show the equivalence of the volt squared per ohm unit and watts. So I have separated them on each side of this table and on the right hand side, we can do some manipulations and we will turn watts into joules per second because that's what watts mean— it's the rate at which energy is used or produced. And on the left side, we will substitute the ohms with volts per current because we have this familiar Ohm's law—V equals IR— which can be rearranged to solve for R by dividing both sides by I in which case resistance is volts per current or in other words, ohm's equals volts divided by current. Okay! It's confusing to divide a fraction by a fraction so instead I am gonna multiply it by the reciprocal of this fraction so I flipped it over and multiplied by it and it's easier to see that this V cancels with one of the V's there leaving us with IV, which is one of our formulas for power. Then replacing current with coulombs per second and volts with joules per coulomb, coulombs cancel leaving us with joules per second and now the left side equals the right side and we say quiet easily done (QED)! We have demonstrated that these units are equivalent because we changed them into things that look the same.