Question
Assume the mostly infrared radiation from a heat lamp acts like a continuous wave with wavelength . (a) If the
lamp’s 200-W output is focused on a person’s shoulder, over a circular area 25.0 cm in diameter, what is the intensity in ? (b) What is the peak electric field strength? (c) Find the peak magnetic field strength. (d) How long will it take to increase the temperature of the 4.00-kg shoulder by , assuming no other heat transfer and given that its specific heat is ?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 42 (Problems & Exercises)

vote with a rating of
votes with an average rating of
.
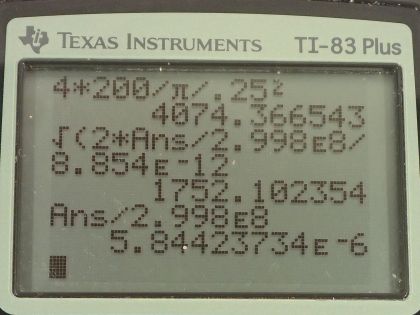
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. A 200 watt heat lamp emits electromagnetic radiation with a wavelength of 1.50 micrometers, which is 1.50 times 10 to the minus 6 meters and it is focused on a spot which is circular shaped with a diameter of 25.0 centimeters which is 0.250 meters. Question (a) is asking what is the intensity of this radiation and so we take its power divided by the area over which it is spread. So it's the area of a circle which is π times its radius squared but we are given diameter instead of radius so we substitute diameter divided by 2 in place of r then we have area then is π times diameter squared over 4 and we are going to divide this power by this fraction and it gets a bit messy to divide a fraction by a fraction so instead I am going to multiply by the reciprocal of this fraction which means multiply by this flipped over so we have power multiplied by 4 over π times diameter squared. That's 4 times 200 watts divided by π times 0.250 meter squared and that's 4.07 times 10 to the 3 watts per square meter intensity. Part (b) is asking us what is the peak electric field strength of this infrared light? Well the average intensity is speed of light times permittivity of free space times peak electric field strength squared over 2 and we know everything in this equation except for E naught and so we are gonna solve for that. We are taking the average intensity to be this intensity that we calculated in part (a). So we have 2 divided by c times ε naught we are multiplying both sides by that and then we solve for peak electric field strength squared that is 2 times intensity divided by speed of light times permittivity of free space and then take the square root of both sides to solve for E naught. So the peak electric field strength is the square root of 2 times the intensity we calculated in part (a) divided by the speed of light times the permittivity of free space and that is 1.75 times 10 to the 3 newtons per coulomb. You could also write units of volts per meter for electric field as well. Part (c) is asking for the magnetic field strength and... there's two ways to do this: you could say that the average intensity is speed of light times peak magnetic field strength squared divided by 2 times permeability of free space and then solve for B naught in the similar way that we did to solve for E naught in part (b) or we can use this formula which says that the peak electric field strength divided by the peak magnetic field strength equals the speed of light and solve this for B naught and that's what we are gonna do because it's a little bit faster. So we multiply both sides by B naught over c and we have the peak magnetic field strength then is the peak electric field strength of 1.7521 times 10 to the 3 newtons per coulomb divided by the speed of light and that is 5.84 times 10 to the minus 6 tesla. Part (d) of this question is asking how long will it take to increase the temperature of 4.00 kilograms of shoulder mass by 2.00 Celsius degree and it gives us the specific heat of the shoulder as well. So power is the rate of heat transfer in this case and so that's the amount of heat divided by time and we can solve for t by multiplying both sides by t divided by power and we have time then is the heat divided by the power. The power we are given—that's 200 watts— and the heat required is gonna equal mass times specific heat times change in temperature; this is a formula from some chapter way back... maybe chapter 14 or something like that. So we have a mass of 4.00 kilograms times a specific heat of 3.47 times 10 to the 3 joules per kilogram per Celsius degree times 2.00 Celsius degrees— temperature change— divided by 200 watts of power and that is 139 seconds.