Question
Lasers can be constructed that produce an extremely high intensity electromagnetic wave for a brief time—called pulsed lasers. They are used to ignite nuclear fusion, for example. Such a laser may produce an electromagnetic wave with a maximum electric field strength of for a time of 1.00 ns. (a) What is the maximum magnetic field strength in the wave? (b) What is the intensity of the beam? (c) What energy does it deliver on a area?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 36 (Problems & Exercises)
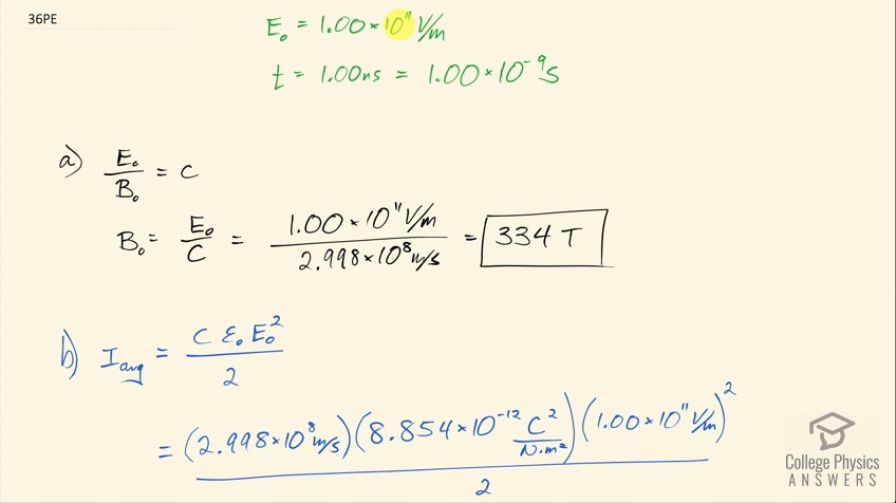
vote with a rating of
votes with an average rating of
.
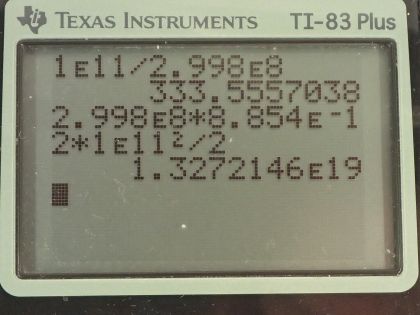
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. The electromagnetic radiation from a pulse laser has a maximum electric field strength of 1.00 times 10 to the 11 volts per meter and the light is being emitted for 1.00 nanosecond, which is 1.00 times 10 to the minus 9 seconds. Part (a) is asking for the peak magnetic field strength. So we know that the ratio of the electric field strength to the magnetic field strength is the speed of the wave which is c—speed of light— and we can solve for B naught by multiplying both sides by B naught over c. So B naught equals E naught over c so that's 1.00 times 10 to the 11 volts per meter divided by 2.998 times 10 to the 8 meters per second and that's 334 tesla. Part (b) is asking what is the intensity of the beam? So the average intensity is speed of light times permittivity of free space times the maximum electric field strength squared divided by 2. So we plug in numbers here: we have speed of light times permittivity of free space and the maximum electric field strength is 1.00 times 10 to the 11 volts per meter and we square that and divide by 2 and we get 1.33 times 10 to the 19 watts per square meter. And then part (c) is asking what energy does it deliver on a 1.00 square millimeter area? So the energy is the power multiplied by the time so this is watts, which is joules per second so this is energy per time and then we are multiplying that by time and we are gonna end up with energy here. The power is the intensity multiplied by the area because intensity is the power per area or watts per square meter in other words then we are multiplying that by an area and we end up with watts. So we substitute IA in place of P and so we have the energy then is the intensity times the area times time. So the intensity we calculated previously here in part (b) 1.3272 times 10 to the 19 watts per square meter and we are multiplying that by the area which we are told is 1.00 square millimeter which we have to convert into square meters by multiplying by 1 meter for every 1000 millimeter and we do that twice and then multiply by the time, which is 1.00 nanosecond and this works out to 13.3 kilojoules.