Question
What capacitance is needed in series with an inductor to form a circuit that radiates a wavelength of 196 m?
Final Answer
Solution video
OpenStax College Physics, Chapter 24, Problem 40 (Problems & Exercises)
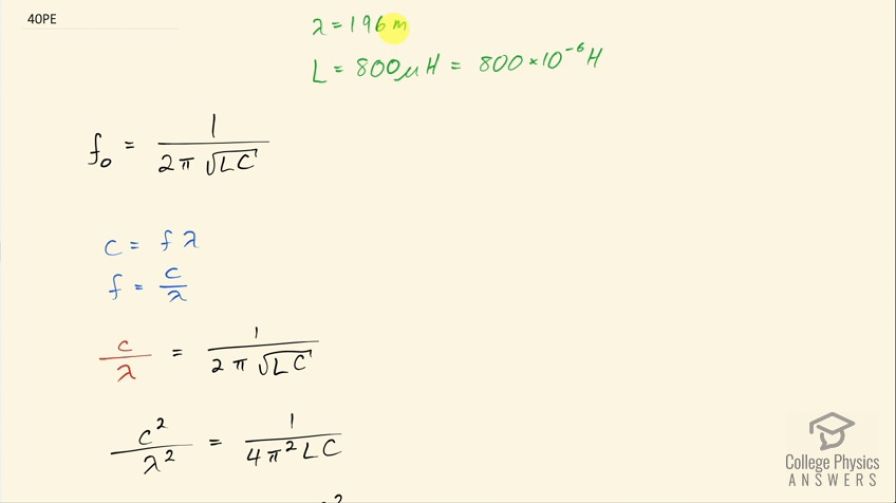
vote with a rating of
votes with an average rating of
.
Calculator Screenshots
Video Transcript
This is College Physics Answers with Shaun Dychko. An LC-circuit emits electromagnetic radiation with a wavelength of 196 meters and the inductance is 800 microhenries, which is 800 times 10 to the minus 6 henries and we have to think back to the formula in chapter 23 where we are told that the resonant frequency of a circuit with an inductor and a capacitor is 1 over 2π times the square root of the inductance times the capacitance and then we can use this information about the emitted wavelength to figure out what the frequency is and then substitute and then we'll solve for c eventually. Okay! So the wave equation says that the speed of a wave equals its frequency times its wavelength and we can solve this for f by dividing both sides by λ and then we have an expression for frequency equaling the speed of light divided by the wavelength and then we can substitute that in for this resonant frequency in this formula and we do that here in red. And then we square both sides and we have c squared over λ squared equals 1 over 4π squared times inductance times capacitance. Now it's a little bit confusing... this letter c gets used for a variety of different things... it could be the specific heat capacity, it could be the capacitance or it could be the speed of light... all these things have the letter c; this is meant to be the little letter c representing speed of light and this is a capital C for capacitance. Alrighty! So we are gonna solve for the capacitance and we are going to multiply both sides by capacitance times wavelength squared divided by speed of light squared and so we have capacitance equals the wavelength squared over 4π squared times inductance times speed of light squared. So that's 196 meters squared divided by 4π squared times 800 times 10 to the minus 6 henries times 2.998 times 10 to the 8 meters per second squared and that is 13.5 picofarads and the prefix 'pico' is times 10 to the minus 12.
