Question
Show that, when SI units for and are entered, the units given by the right-hand side of the equation are m/s.
Final Answer
Please see the solution video.
Solution video
OpenStax College Physics, Chapter 24, Problem 2 (Problems & Exercises)
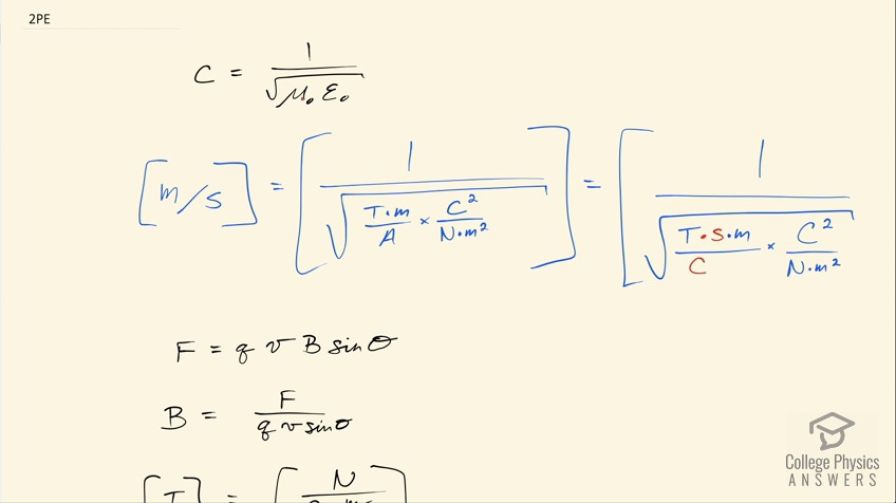
vote with a rating of
votes with an average rating of
.
Video Transcript
This is College Physics Answers with Shaun Dychko. The speed of light is given by this formula 1 over the square root of the permeability of free space multiplied by the permittivity of free space and we are going to check that the units on the left and the right side of this equation are the same as they should be. So on the left side, it's a speed so that's meters per second and on the right side, we have 1 over the square root of tesla meters per amp, which are the units of permeability of free space and coulomb squared per newton meters squared, which is the units for permittivity of free space. So now our work involves translating some of these units into other things that can cancel and so on and we need to be left with meters per second on this right hand side somehow. Let's first turn this amps into coulombs per second and since we are dividing by coulombs per second, we can instead multiply this by seconds per coulomb and we also need to deal with this tesla so let us figure out what units the tesla can be turned into. I looked at this formula here, which says that the force is the charge multiplied by its speed times the magnetic field strength times the sin of the angle between the velocity and the field and we can rearrange this to solve for B and so this gives us some units for tesla now because on the left side, we have tesla and on the right hand side, we have newtons from this force divided by coulombs from the factor q and meters per second from v, sin Θ is a ratio and so it has no units and then we can substitute this in place of T where I have written the seconds on the top here by the way when I have done the substitution. So all this stuff in red is just T so that's newton seconds per coulomb meter and then multiplied by the rest of this fraction here which is seconds meters per coulomb so seconds meters per coulomb there times coulomb squared over newton meters squared. Okay! Then we can see that the coulomb squared on the top cancels with the coulomb squared on the bottom, the newtons on the top cancels with the newtons on the bottom and we have seconds squared on the top and we have one meter canceling with one meter below leaving us with meters squared in the denominator here. So this is 1 over seconds per meter when we take the square root of that and 1 over seconds per meter is the reciprocal of seconds per meter, which is meters per second. So there we go! We have shown that the units on the right hand side of this equation are the same as the units on the left.